
(08年龙岩一中冲刺理)(12分)
如图,四棱锥P―ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明PA//平面BDE;
(2)求二面角B―DE―C的大小;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
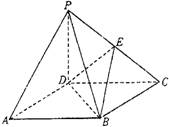
解析:解法一:(1)连结AC,设AC与BD交于O点,连结EO.
由底面ABCD是正方形知O为AC的中点,又E为PC的中点,
|
∴OE//PA, ∵OE![]() 平面BDE,
平面BDE,![]() 平面BDE,
平面BDE,
∴PA//平面BDE ………………4分
(2)∵PD⊥底面ABCD,∴PD⊥BC,又BC⊥CD,
∴BC⊥平面PCD,又PD=DC,E为PC的中点,
∴DE⊥PC,从而由三垂线定理知DE⊥BE,
∴∠BEC是二面角B―DE―C的平面角.
设正方形ABCD的边长为a,
则![]() ,
,
在Rt△BCE中,![]()
∴二面角B―DE―C的大小为![]() …………8分
…………8分
(3)作EF⊥PB于点F,则Rt△PEF∽Rt△PBC,∴![]()
∴PF?PB=PE?PC=![]() ,连结DF
,连结DF
∵在△PBD中,∠PDB=90°,PF?PB=a2=PD2, ∴PB⊥DF,
从而PB⊥平面DEF,此时![]()
即在棱PB上存在点F,![]() ,使得PB⊥平面DEF …………12分
,使得PB⊥平面DEF …………12分
解法二:(1)以D为坐标原点,分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),
B(2,2,0) ![]()
设 ![]() 是平面BDE的一个法向量,
是平面BDE的一个法向量,
则由 
∵![]() ……4分
……4分


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
(08年龙岩一中冲刺文)(12分)
如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 折到点
折到点![]() 的位置,且二面角
的位置,且二面角![]() 的大小为
的大小为![]()
(1)求证:![]()
(2)求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小
(3)求点![]() 到平面
到平面![]() 的距离
的距离

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中冲刺理)(12分)
已知双曲线![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,
,![]() 为动点,若
为动点,若![]() ,
,![]() 为定值(其中
为定值(其中![]() >1),
>1),![]() 的最小值为
的最小值为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设点![]() ,过点
,过点![]() 作直线
作直线![]() 交轨迹
交轨迹![]() 于
于![]() ,
,![]() 两点,判断
两点,判断![]() 的大小是否为定值?并证明你的结论.
的大小是否为定值?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中冲刺理)(14分)
在直角坐标平面xoy上的一列点![]() 简记为
简记为![]() ,若由
,若由![]() 构成的数列
构成的数列![]() 满足
满足![]() 其中
其中![]() 是y轴正方向相同的单位向量,则
是y轴正方向相同的单位向量,则![]() 为T点列.
为T点列.
(1)判断![]() 是否为T点列,并说明理由;
是否为T点列,并说明理由;
(2)若![]() 为T点列,且点
为T点列,且点![]() 在
在![]() 的右上方,任取其中连续三点
的右上方,任取其中连续三点![]() ,判定
,判定![]() 的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;
(3)若![]() 为T点列,正整数
为T点列,正整数![]() 满足
满足![]() .求证:
.求证:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com