
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)如果当![]() ,且
,且![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的范围.
的范围.
【答案】(1)![]() 的单调递增区间
的单调递增区间![]() 和
和![]() ;
;![]() 的单调递减区间
的单调递减区间![]() .
.
(2)实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】分析:(1)求出函数的导数,对![]() 分
分![]() 和
和![]() 两种情况讨论,即可得到函数的单调性;
两种情况讨论,即可得到函数的单调性;
(2)由题意把式子![]() 化为
化为![]() ,设
,设![]() ,
,
由(1)的结论,即可求解实数![]() 的取值范围;或把
的取值范围;或把![]() 可化为
可化为![]() ,设
,设![]() ,求得
,求得![]() 得出函数的单调性,令洛必达法则求解.
得出函数的单调性,令洛必达法则求解.
详解:(1)定义域为![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
①当![]() 时,对称轴
时,对称轴![]() ,
,![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
②当![]() 时,
时,![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
③当![]() 时,令
时,令![]() 得
得![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,
,![]() ;令
;令![]() ,解得
,解得![]() ,
,
所以![]() 的单调递增区间
的单调递增区间![]() 和
和![]() ;
;![]() 的单调递减区间
的单调递减区间![]() .
.
(2)![]() 可化为
可化为![]() ,设
,设![]() ,
,
由(1)知:
①当![]() 时,
时,![]() 在
在![]() 上是增函数,若
上是增函数,若![]() 时,
时,![]() ;
;
所以![]() ,
,
若![]() 时,
时,![]() ,所以
,所以![]() ,所以,当
,所以,当![]() 时,
时,![]() 式成立.
式成立.
②当![]() 时,
时,![]() 在
在![]() 是减函数,所以
是减函数,所以![]() 式不成立,
式不成立,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
解法二:![]() 可化为
可化为![]() ,设
,设
![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ;
;
![]() ,
,![]() 在
在![]() 上,又
上,又![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
所以![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() 在
在![]() ,
,![]() ,
,
由洛必达法则![]()
![]() ,所以
,所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
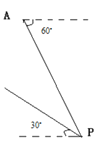
【题目】据监测,在海滨某城市附近的海面有一台风. 台风中心位于城市![]() 的东偏南
的东偏南![]() 方向、距离城市
方向、距离城市![]() 的海面
的海面![]() 处,并以
处,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移动(如图示).如果台风侵袭范围为圆形区域,半径
方向移动(如图示).如果台风侵袭范围为圆形区域,半径![]() ,台风移动的方向与速度不变,那么该城市受台风侵袭的时长为_____ .
,台风移动的方向与速度不变,那么该城市受台风侵袭的时长为_____ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题的序号为__________.
①已知随机变量服从二项分布![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() ;
;
④某人在![]() 次射击中,击中目标的次数为
次射击中,击中目标的次数为![]() ,
,![]() ,则当
,则当![]() 时概率最大.
时概率最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料90 ![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1 ![]() ,五合板2
,五合板2 ![]() ,生产每个书橱需要方木料0.2
,生产每个书橱需要方木料0.2![]() ,五合板1
,五合板1 ![]() ,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大?
,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年北京国际数学家大会会标,是以中国古代数学家赵爽的弦图为基础而设计的,弦图用四个全等的直角三角形与一个小正方形拼成的一个大正方形![]() 如图
如图![]() ,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为
,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为![]() ,则
,则![]() 等于
等于![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(sinx+cosx)﹣ ![]() .
.
(1)若0<α< ![]() ,且sinα=
,且sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com