练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    　　已知在△ABC中，三个内角A，B，C成等差数列且A＜B＜C，tanA·tanC=,求角A，B，C的值。

     

    答案：
    解析：

    		　　解：由已知，有A+B+C=，2B=A+C。

    　　∴B=，A+C=

    　　∴tan，即

    　　∵tan,∴

    　　∴tanA,tanC是方程的两个根。

    　　解得t=1或t=

    　　又∵A＜C，∴tanA=1,tanC=

    　　而＜A＜,＜C＜,

    　　∴A=,C=--=

    　　故角A,B,C的值分别为,,.

    　　注:此题具有一定的综合性,除了应具备三角形,数列及三角公式等知识外,方程思想的体现(得到以tanA,tanC为未知数的方程组)与应用也是十分关键的.

     


    提示：

    		　　分析：在△ABC中，首先有A+B+C=180°，又三内角成等差数列。

    　　∴2B=A+C，因此B=，A+C=，又tanA·tanC=,可求tanA+tanC,进而求tanA,tanC再求出A，C

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知在△ABC中，∠ACB=90°，BC=4，AC=3，P是AB上一点，则点P到AC，BC的距离乘积的最大值是（　　）
    A、2B、3C、4D、5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

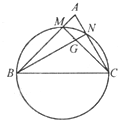    （2013•成都一模）如图，已知在△ABC中，BC=2，以BC为直径的圆分别交AB，AC于点M，N，MC与NB交于点G，若
    BM
    •
    BC
    =2    ，
    CN
    •
    BC
    =-1    ，则∠BGC的度数为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知在△ABC中，AB=AC=2，BC=2
    		3
    ，点P为边BC所在直线上的一个动点，则关于
    AP
    ?(
    AB
    +
    AC
    )    的值，正确的是（　　）
    A、为定值2
    B、最大值为4
    C、最小值为1
    D、与P的位置有关

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    　　已知在△ABC中，三个内角A，B，C成等差数列且A＜B＜C，tanA·tanC=,求角A，B，C的值。

     

    查看答案和解析>>

    同步练习册答案