
°æƒø°øƒ≥–£∏fl“ª£®2£©∞‡π≤”–60√˚Õ¨—ß≤Œº”∆⁄ƒ©øº ‘£¨œ÷Ω´∆‰ ˝—ß—ßø∆≥…º®£®æ˘Œ™’˚ ˝£©∑÷≥…¡˘∏ˆ∑÷ ˝∂Œ![]() £¨
£¨ ![]() £¨°≠£¨
£¨°≠£¨ ![]() £¨ª≠≥ˆ»Áœ¬ÕºÀ˘ 浃≤ø∑÷∆µ¬ ∑÷≤º÷±∑ΩÕº£¨«Îπ€≤ÏÕº–Œ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£¨ª≠≥ˆ»Áœ¬ÕºÀ˘ 浃≤ø∑÷∆µ¬ ∑÷≤º÷±∑ΩÕº£¨«Îπ€≤ÏÕº–Œ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
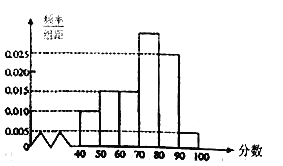
£®1£©π¿º∆’‚¥Œøº ‘÷– ˝—ß—ßø∆≥…º®µƒ÷–Œª ˝£ª
£®2£©œ÷∏˘æ›±æ¥Œøº ‘∑÷ ˝∑÷≥…œ¬¡–¡˘∂Œ£®¥”µÕ∑÷∂ŒµΩ∏fl∑÷∂Œ“¿¥ŒŒ™µ⁄“ª◊È°¢µ⁄∂˛◊È°¢°≠°¢µ⁄¡˘◊È£©Œ™Ã·∏fl±æ∞‡ ˝—ß’˚ÃÂ≥…º®£¨æˆ∂®◊È”Î◊È÷ƺ‰Ω¯––∞Ô∑ˆ—ßœ∞.»Ù—°≥ˆµƒ¡Ω◊È∑÷ ˝÷Æ≤Ó¥Û”⁄30∑÷£®“‘∑÷ ˝∂ŒŒ™“¿æ›£¨≤ª“‘æfl×߅˙∑÷ ˝Œ™“¿æ›£©£¨‘Ú≥∆’‚¡Ω◊ÈŒ™°∞◊Óº—◊È∫œ°±£¨ ‘«Û—°≥ˆµƒ¡Ω◊ÈŒ™°∞◊Óº—◊È∫œ°±µƒ∏≈¬ .
°æ¥∞∏°ø(1) ÷–Œª ˝Œ™![]() ;(2)
;(2) ![]() .
.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©∏˘æ›∆µ¬ ∑÷≤º÷±∑ΩÕº£¨¿˚”√÷–Œª ˝µƒº∆À„∑Ω∑®£¨º¥ø…µ√µΩ÷–Œª ˝µƒ÷µ£ª
£®2£©¡–≥ˆÀ˘”–µƒ◊È∫œ ˝£¨µ√µΩª˘±æ ¬º˛µƒ∏ˆ ˝£¨‘Ÿ∏˘æ›π≈µ‰∏≈–Õµƒ∏≈¬ º∆À„π´ Ω£¨º¥ø…«ÛΩ‚—°≥ˆµƒ¡Ω◊ÈŒ™°∞◊Óº—◊È∫œ°±µƒ∏≈¬ .
‘Ã‚Ω‚Œˆ£∫
£®1£©÷–Œª ˝‘⁄![]() ƒ⁄.÷–Œª ˝Œ™
ƒ⁄.÷–Œª ˝Œ™![]()
£®2£©À˘”–µƒ◊È∫œ ˝£∫£®1,2£©£¨£®1,3£©£¨£®1,4£©£¨£®1,5£©£¨£®1,6£©
£®2,3£©£¨£®2,4£©£¨£®2,5£©£¨£®2,6£©
£®3,4£©£¨£®3,5£©£¨£®3,6£©
£®4,5£©£¨£®4,6£©
£®5,6£©
![]() £¨
£¨
∑˚∫œ°∞◊Óº—◊È∫œ°±Ãıº˛µƒ”–£∫£®1,4£©£¨£®1,5£©£¨£®1,6£©£¨£®2,5£©£¨£®2,6£©£¨£®3,6£©
![]() £¨À˘“‘
£¨À˘“‘![]() .
.


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
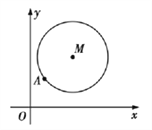
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨“—÷™“‘
÷–£¨“—÷™“‘![]() Œ™‘≤–ƒµƒ‘≤
Œ™‘≤–ƒµƒ‘≤![]() £∫
£∫![]() º∞∆‰…œ“ªµ„
º∞∆‰…œ“ªµ„![]() .
.
£®1£©…Ë‘≤![]() ”Î
”Î![]() ÷·œ‡«–£¨”Α≤
÷·œ‡«–£¨”Α≤![]() Õ‚«–£¨«“‘≤–ƒ
Õ‚«–£¨«“‘≤–ƒ![]() ‘⁄÷±œfl
‘⁄÷±œfl![]() …œ£¨«Û‘≤
…œ£¨«Û‘≤![]() µƒ±Í◊º∑Ω≥ãª
µƒ±Í◊º∑Ω≥ãª
£®2£©…Ë∆Ω––”⁄![]() µƒ÷±œfl
µƒ÷±œfl![]() ”Α≤
”Α≤![]() œ‡Ωª”⁄
œ‡Ωª”⁄![]() £¨
£¨![]() ¡Ωµ„£¨«“
¡Ωµ„£¨«“![]() £¨«Û÷±œfl
£¨«Û÷±œfl![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®3£©…˵„![]() ¬˙◊„£∫¥Ê‘⁄‘≤
¬˙◊„£∫¥Ê‘⁄‘≤![]() …œµƒ¡Ωµ„
…œµƒ¡Ωµ„![]() ∫Õ
∫Õ![]() £¨ πµ√
£¨ πµ√![]() £¨«Û µ ˝
£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø—°–fi4-5£∫≤ªµ» Ω—°Ω≤
“—÷™≤ªµ» Ω![]()
![]() ∂‘»Œ“‚ µ ˝
∂‘»Œ“‚ µ ˝![]() ∫„≥…¡¢£Æ
∫„≥…¡¢£Æ
£®¢Ò£©«Û µ ˝![]() µƒ◊Ó–°÷µ
µƒ◊Ó–°÷µ![]() £ª
£ª
£®¢Ú£©»Ù![]() £¨«“¬˙◊„
£¨«“¬˙◊„![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë’˝œÓ ˝¡–{an}µƒ«∞nœÓ∫ÕŒ™Sn £¨ «“¬˙◊„4Sn=an2+2an©Å3£®n° N*£©£¨‘Úa2016=£® £©
A.4029
B.4031
C.4033
D.4035
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø’˝œÓ ˝¡–{an}µƒ«∞nœÓ∫ÕŒ™Sn £¨ «“2Sn=an2+an£®n° N*£©£¨…Ëcn=£®©Å1£©n ![]() £¨‘Ú ˝¡–{cn}µƒ«∞2017œÓµƒ∫ÕŒ™ £Æ
£¨‘Ú ˝¡–{cn}µƒ«∞2017œÓµƒ∫ÕŒ™ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ≥§∞Î÷·Œ™
µƒ≥§∞Î÷·Œ™![]() £¨∂Ã∞Î÷·Œ™
£¨∂Ã∞Î÷·Œ™![]() .Õ÷‘≤
.Õ÷‘≤![]() µƒ¡Ω∏ˆΩπµ„∑÷±Œ™
µƒ¡Ω∏ˆΩπµ„∑÷±Œ™![]() £¨
£¨![]() £¨¿Î–ƒ¬ Œ™∑Ω≥Ã
£¨¿Î–ƒ¬ Œ™∑Ω≥Ã![]() µƒ“ª∏˘£¨≥§∞Î÷·Œ™
µƒ“ª∏˘£¨≥§∞Î÷·Œ™![]() £¨∂Ã∞Î÷·Œ™
£¨∂Ã∞Î÷·Œ™![]() .»Ù
.»Ù![]() £¨
£¨![]() .
.
£®¢Ò£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
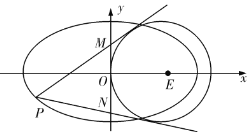
£®¢Ú£©»ÁÕº£¨π˝Õ÷‘≤![]() …œ«“Œª”⁄
…œ«“Œª”⁄![]() ÷·◊Û≤‡µƒ“ªµ„
÷·◊Û≤‡µƒ“ªµ„![]() ◊˜‘≤
◊˜‘≤![]()
![]() µƒ¡ΩÃı«–œfl£¨∑÷±Ωª
µƒ¡ΩÃı«–œfl£¨∑÷±Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() °¢
°¢![]() £Æ ‘Õ∆∂œ «∑ҥʑ⁄µ„
£Æ ‘Õ∆∂œ «∑ҥʑ⁄µ„![]() £¨ π
£¨ π![]() £ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„
£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø—°–fi4-4£∫◊¯±Íœµ”Î≤Œ ˝∑Ω≥Ã
‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨÷±œfl
÷–£¨÷±œfl![]() µƒ≤Œ ˝∑Ω≥ÃŒ™
µƒ≤Œ ˝∑Ω≥ÃŒ™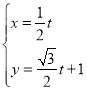 £®
£®![]() Œ™≤Œ ˝£©£¨«˙œfl
Œ™≤Œ ˝£©£¨«˙œfl![]() µƒ∆’Õ®∑Ω≥ÃŒ™
µƒ∆’Õ®∑Ω≥ÃŒ™![]() £¨“‘◊¯±Í‘≠µ„Œ™º´µ„£¨
£¨“‘◊¯±Í‘≠µ„Œ™º´µ„£¨![]() ÷·µƒ’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£Æ
÷·µƒ’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£Æ
£®I£©«Û÷±œfl![]() µƒº´◊¯±Í∑Ω≥ÔΫ˙œfl
µƒº´◊¯±Í∑Ω≥ÔΫ˙œfl![]() µƒ≤Œ ˝∑Ω≥ãª
µƒ≤Œ ˝∑Ω≥ãª
£®II£©…˵„D‘⁄«˙œfl![]() …œ£¨«“«˙œfl
…œ£¨«“«˙œfl![]() ‘⁄µ„D¥¶µƒ«–œfl”Î÷±œfl
‘⁄µ„D¥¶µƒ«–œfl”Î÷±œfl![]() ¥π÷±£¨ ‘»∑∂®µ„Dµƒ◊¯±Í.
¥π÷±£¨ ‘»∑∂®µ„Dµƒ◊¯±Í.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() æ≠π˝µ„
æ≠π˝µ„![]() £¨«“¿Î–ƒ¬ Œ™
£¨«“¿Î–ƒ¬ Œ™![]() .
.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©…˵„![]() ‘⁄
‘⁄![]() ÷·…œµƒ…‰”∞Œ™µ„
÷·…œµƒ…‰”∞Œ™µ„![]() £¨π˝µ„
£¨π˝µ„![]() µƒ÷±œfl
µƒ÷±œfl![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() œ‡Ωª”⁄
œ‡Ωª”⁄![]() £¨
£¨ ![]() ¡Ωµ„£¨«“
¡Ωµ„£¨«“![]() £¨«Û÷±œfl
£¨«Û÷±œfl![]() µƒ∑Ω≥Ã.
µƒ∑Ω≥Ã.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨«“π˝µ„
£¨«“π˝µ„![]() .
.

£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©π˝µ„![]() «“–±¬ ¥Û”⁄0µƒ÷±œfl
«“–±¬ ¥Û”⁄0µƒ÷±œfl![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() œ‡Ωª”⁄µ„
œ‡Ωª”⁄µ„![]() £¨
£¨ ![]() £¨÷±œfl
£¨÷±œfl![]() £¨
£¨ ![]() ”Î
”Î![]() ÷·œ‡Ωª”⁄
÷·œ‡Ωª”⁄![]() £¨
£¨ ![]() ¡Ωµ„£¨«Û
¡Ωµ„£¨«Û![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com