
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
【答案】(1)![]() ;(2)是定值,其定值为
;(2)是定值,其定值为![]() .
.
【解析】
(1)设椭圆![]() 的焦距为
的焦距为![]() ,根据题意得出关于
,根据题意得出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 和
和![]() 的值,即可得出椭圆
的值,即可得出椭圆![]() 的标准方程;
的标准方程;
(2)对直线![]() 的斜率是否存在进行分类讨论,当直线
的斜率是否存在进行分类讨论,当直线![]() 轴时,可得出直线
轴时,可得出直线![]() 的方程为
的方程为![]() ,可求出四边形
,可求出四边形![]() 的面积;当直线
的面积;当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,求出点
的方程联立,列出韦达定理,求出点![]() 的坐标,将点
的坐标,将点![]() 的坐标代入椭圆
的坐标代入椭圆![]() 的方程得出
的方程得出![]() ,计算出
,计算出![]() 以及原点
以及原点![]() 到直线
到直线![]() 的距离,通过化简计算可得出四边形
的距离,通过化简计算可得出四边形![]() 的面积为
的面积为![]() ,进而得证.
,进而得证.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,由题意可得
,由题意可得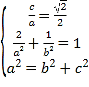 ,解得
,解得![]() ,
,![]() ,
,
因此,椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
若直线![]() 的方程为
的方程为![]() ,联立
,联立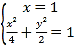 ,可得
,可得 ,
,
此时,![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,
,
同理,当直线![]() 的方程为
的方程为![]() 时,可求得四边形
时,可求得四边形![]() 的面积也为
的面积也为![]() ;
;
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程是
方程是![]() ,
,
代人到![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,
,
![]() 点
点![]() 在椭圆
在椭圆![]() 上,所以有
上,所以有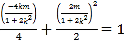 ,整理得
,整理得![]() ,
,
由题意知,四边形![]() 为平行四边形,
为平行四边形,
![]() 平行四边形
平行四边形![]() 的面积为
的面积为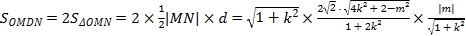
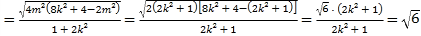 .
.
故四边形![]() 的面积是定值,其定值为
的面积是定值,其定值为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户考察三种不同的果树苗A、B、C,经引种试验后发现,引种树苗A的自然成活率为0.8,引种树苗B、C的自然成活率均为0.9.
(1)若引种树苗A、B、C各10棵.
①估计自然成活的总棵数;
②利用①的估计结论,从没有自然成活的树苗中随机抽取两棵,求抽到的两棵都是树苗A的概率;
(2)该农户决定引种B种树苗,引种后没有自然成活的树苗中有75%的树苗可经过人工栽培技术处理,处理后成活的概率为0.8,其余的树苗不能成活.若每棵树苗引种最终成活后可获利300元,不成活的每棵亏损50元,该农户为了获利不低于20万元,问至少引种B种树苗多少棵?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动圆![]() 与
与![]() 相外切,与
相外切,与![]() 相内切.
相内切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)![]() 是动圆
是动圆![]() 的半径最小时的圆,倾斜角为
的半径最小时的圆,倾斜角为![]() 且过点
且过点![]() 的直线l与
的直线l与![]() 相切,与轨迹
相切,与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,书中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”,该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚减一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数![]() 是8的整数倍时,均可采用此方法求解,如图是解决这类问题的程序框图,若输入
是8的整数倍时,均可采用此方法求解,如图是解决这类问题的程序框图,若输入![]() ,则输出的结果为( )
,则输出的结果为( )
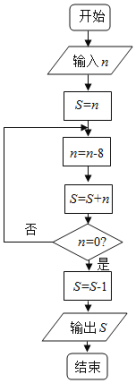
A.80B.47C.79D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:

表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:
![]()
如果把5根算筹以适当的方式全部放入 下面的表格中,那么可以表示的三位数的个数为( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物兴趣小组对冬季昼夜温差与反季节新品种大豆发芽数之间的关系进行研究,他们分别记录了![]() 月
月![]() 日至
日至![]() 月
月![]() 日每天的昼夜温差与实验室每天
日每天的昼夜温差与实验室每天![]() 颗种子的发芽数,得到以下表格
颗种子的发芽数,得到以下表格

该兴趣小组确定的研究方案是:先从这![]() 组数据中选取
组数据中选取![]() 组数据,然后用剩下的
组数据,然后用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1) 求统计数据中发芽数的平均数与方差;
(2) 若选取的是![]() 月
月![]() 日与
日与![]() 月
月![]() 日的两组数据,请根据
日的两组数据,请根据![]() 月
月![]() 日至
日至![]() 月
月![]() 日的数据,求出发芽数
日的数据,求出发芽数![]() 关于温差
关于温差![]() 的线性回归方程
的线性回归方程![]() ,若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过
,若由线性回归方程得到的估计数据与所选取的检验数据的误差不超过![]() ,则认为得到的线性回归方程是可靠的,问得到的线性回归方程是否可靠? 附:线性回归方程
,则认为得到的线性回归方程是可靠的,问得到的线性回归方程是否可靠? 附:线性回归方程![]() 中斜率和截距最小二乘估法计算公式:
中斜率和截距最小二乘估法计算公式:
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若直线![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 被椭圆
被椭圆![]() 所截得的弦的长度;
所截得的弦的长度;
(2)若已知点![]() 在椭圆
在椭圆![]() 上,动点
上,动点![]() 满足
满足![]() ,请判断点
,请判断点![]() 与圆
与圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com