
分析 根据三角函数f(x)=sin(2x+$\frac{π}{3}$)在x∈[0,π]的图象与性质,即可求出对任意的x1,x2,x3,且0≤x1<x2<x3≤π时,
|f(x1)-f(x2)|+|f(x2)-f(x3)|的最大值,从而求出实数m的最小值.
解答 解:函数f(x)=sin(2x+$\frac{π}{3}$),其中x∈[0,π],
∴2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{3}$],
∴-1≤f(x)≤1;
又对任意的x1,x2,x3,且0≤x1<x2<x3≤π,
都有|f(x1)-f(x2)|+|f(x2)-f(x3)|≤m成立,
不妨令f(x2)=-1,则:
当f(x1)=1、f(x3)=$\frac{\sqrt{3}}{2}$时,
|f(x1)-f(x2)|+|f(x2)-f(x3)|取得最大值为2+1+$\frac{\sqrt{3}}{2}$=3+$\frac{\sqrt{3}}{2}$;
∴实数m的最小值为3+$\frac{\sqrt{3}}{2}$.
故答案为:3+$\frac{\sqrt{3}}{2}$.
点评 本题考查了三角函数的图象与性质的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{{e}^{3}}$,$\frac{1}{{e}^{2}}$) | B. | ($\frac{1}{{e}^{2}}$,$\frac{1}{e}$) | C. | ($\frac{1}{e}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
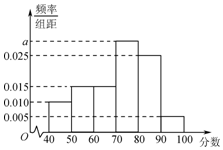 某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com