
| A. | (¬p)∧q | B. | p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
分析 先判断命题p和命题q的真假,进而根据复合命题真假判断的真值表,得到答案.
解答 解:函数$f(x)=\frac{2x+3}{x}$=$\frac{3}{x}$+2的图象由函数y=$\frac{3}{x}$的图象向上平移两个单位得到,
故关于(0,2)中心对称;
故命题p:函数$f(x)=\frac{2x+3}{x}$的图象关于(0,3)中心对称为假命题;
若函数g(x)=msinx+ncosx(m,n∈R)满足$g({\frac{π}{6}-x})=g({\frac{π}{6}+x})$,
则函数图象关于直线x=$\frac{π}{6}$对称,
则g($\frac{π}{6}$)=msin$\frac{π}{6}$+ncos$\frac{π}{6}$=±$\sqrt{{m}^{2}+{n}^{2}}$,
解得:$n=\sqrt{3}m$,
故命题q为真命题,
故命题(¬p)∧q为真命题,
命题p∧q,p∨(¬q),(¬p)∧(¬q)为假命题;
故选:A
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的对称性,三角函数的化简求值等知识点,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
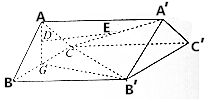 已知正三棱柱ABC-A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4.
已知正三棱柱ABC-A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为24$\sqrt{2}$.
如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为24$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果a>b,那么$\frac{a}{c}$>$\frac{b}{c}$ | B. | 如果ac<bc,那么a<b | ||
| C. | 如果a>b,c>d,那么a-c>b-d | D. | 如果a>b,那么a-c>b-c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com