
【题目】如图①,△ABC是以AC为斜边的等腰直角三角形,△BCD是等边三角形.如图②,将△BCD沿BC折起,使平面BCD⊥平面ABC,记BC的中点为E,BD的中点为M,点F、N在棱AC上,且AF=3CF,C![]() .
.
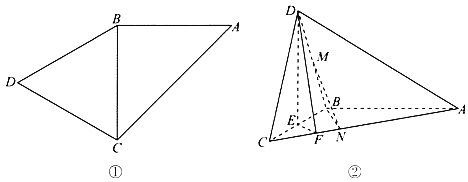
(1)试过直线MN作一平面,使它与平面DEF平行,并加以证明;
(2)记(1)中所作的平面为α,求平面α与平面BMN所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)过![]() 作
作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,推导出
,推导出![]() 是
是![]() 的中点,从而
的中点,从而![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过点
轴,过点![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,利用向量法能求出平面
轴,建立空间直角坐标系,利用向量法能求出平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)过N作NG∥EF,交BC于G,连结MG,则平面MNG∥平面DEF.
理由如下:
∵EF∥NG,BC的中点为E,BD的中点为M,点F、N在棱AC上,且AF=3CF,
C![]() .
.
∴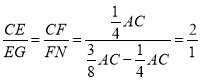 ,
,
∴G是BE的中点,
∴MG∥DE,又DE∩EF=E,MG∩NG=G,
∴平面MNG∥平面DEF.
(2)以B为原点,BC为x轴,BA为y轴,过点B作平面ABC的垂线为z轴,建立空间直角坐标系,如下图所示:
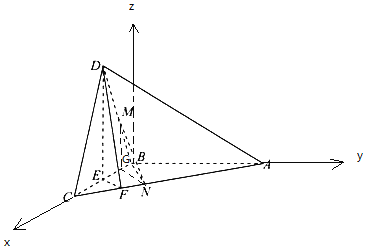
设BC=2,则B(0,0,0),D(1,0,![]() ),M(
),M(![]() ),
),
A(0,2,0),G(![]() ,0,0),N(
,0,0),N(![]() ,
,![]() ,0),
,0),
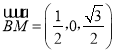 ,
,![]() ,
,![]() (0,0,
(0,0,![]() ,
,![]() ,0
,0![]() ,
,
设平面BMN的法向量![]() (x,y,z),
(x,y,z),
则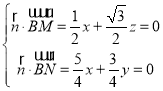 ,取
,取![]() ,得
,得![]() ,
,![]() ,﹣1
,﹣1![]() ,
,
设平面GMN的法向量![]() (x,y,z),
(x,y,z),
则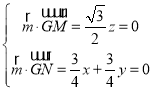 ,取x=1,得
,取x=1,得![]() (1,﹣1,0),
(1,﹣1,0),
设平面α与平面BMN所成锐二面角的平面角为θ,
则cosθ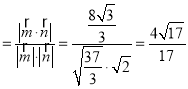 .
.
∴平面α与平面BMN所成锐二面角的余弦值为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:
【题目】为了研究每周累计户外暴露时间是否足够(单位:小时)与近视发病率的关系,对某中学一年级![]() 名学生进行不记名问卷调查,得到如下数据:
名学生进行不记名问卷调查,得到如下数据:

(1)用样本估计总体思想估计该中学一年级学生的近视率;
(2)能否认为在犯错误的概率不超过![]() 的前提下认为不足够的户外暴露时间与近视有关系?
的前提下认为不足够的户外暴露时间与近视有关系?
附: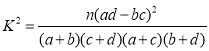 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()
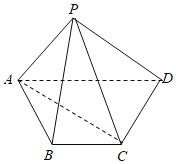
(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
(1)求这1000名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表. 请将列联表补充完整,并根据列联表判断是否有![]() 的把握认为潜伏期与患者年龄有关;
的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) |
| ||
50岁以下 | 55 | ||
总计 | 200 |
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立. 为了深入研究,该研究团队随机调查了![]() 名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
|
|
| |
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉,字谦光,南宋时期杭州人.在他1261年所著的《详解九章算法》一书中,辑录了如图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”.故此,杨辉三角又被称为“贾宪三角”.杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
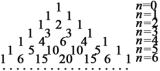
基于上述规律,可以推测,当![]() 时,从左往右第22个数为_____________.
时,从左往右第22个数为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为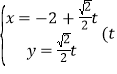 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com