
【题目】解答题。
(1)解方程4x﹣2x﹣2=0.
(2)求不等式 log2(2x+3)>log2(5x﹣6);
(3)求函数y=( ![]() )
) ![]() ,x∈[0,5)的值域.
,x∈[0,5)的值域.
【答案】
(1)解:原方程可化为(2x)2﹣2x﹣2=0.
令2x=t,则t>0,所以t2﹣t﹣2=0,
解得t=2或t=﹣1(舍).
由2x=2解得x=1
(2)解:原不等式等价于 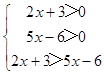 ,解得
,解得 ![]() <x<3,
<x<3,
∴原不等式的解集为( ![]() ,3)
,3)
(3)解:令u=x2﹣4x,x∈[0,5),则﹣4≤u<5,
则 ![]() ,即
,即 ![]() .
.
即值域为( ![]() ]
]
【解析】(1)利用换元法化圆方程为一元二次方程求解;(2)直接利用对数函数的单调性化对数不等式为一元一次不等式组求解;(3)令u=x2﹣4x换元,由x得范围求得u的范围,再由指数函数的单调性得答案.
【考点精析】解答此题的关键在于理解指、对数不等式的解法的相关知识,掌握指数不等式的解法规律:根据指数函数的性质转化;对数不等式的解法规律:根据对数函数的性质转化.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知销售“笔记本电脑”和“台式电脑”所得的利润分别是P(单位:万元)和Q(单位:万元),它们与进货资金t(单位:万元)的关系有经验公式P= ![]() t和Q=
t和Q= ![]()
![]() .某商场决定投入进货资金50万元,全部用来购入这两种电脑,那么该商场应如何分配进货资金,才能使销售电脑获得的利润y(单位:万元)最大?最大利润是多少万元?
.某商场决定投入进货资金50万元,全部用来购入这两种电脑,那么该商场应如何分配进货资金,才能使销售电脑获得的利润y(单位:万元)最大?最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.在△ABC中,角A,B,C的对边分别是a,b,c,则a>b是cos A<cos B的充要条件
B.命题p:对任意的x∈R,x2+x+1>0,则¬p:对任意的x∈R,x2+x+1≤0
C.已知p: ![]() >0,则¬p:
>0,则¬p: ![]() ≤0
≤0
D.存在实数x∈R,使sin x+cos x= ![]() 成立
成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,并根据 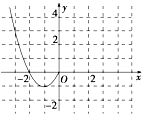
(1)写出函数f(x)(x∈R)的增区间;
(2)写出函数f(x)(x∈R)的解析式;
(3)若函数g(x)=f(x)﹣2ax+2(x∈[1,2]),求函数g(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设O是平行四边形ABCD的两条对角线AC,BD的交点,下列向量组:
① ![]() 与
与 ![]() ;②
;② ![]() 与
与 ![]() ;
;
③ ![]() 与
与 ![]() ;④
;④ ![]() 与
与 ![]() .
.
其中可作为这个平行四边形所在平面的一组基底的是( ).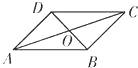
A.①②
B.③④
C.①③
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位,得到函数y=f(x)的图象,则下列关于函数y=f(x)的说法正确的是( )
个单位,得到函数y=f(x)的图象,则下列关于函数y=f(x)的说法正确的是( )
A.奇函数
B.周期是 ![]()
C.关于直线 ![]() 对称
对称
D.关于点 ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图所示,一根水平放置的长方体枕木的安全负荷与它的厚度d的平方和宽度a的乘积成正比,同时与它的长度![]() 的平方成反比.
的平方成反比.
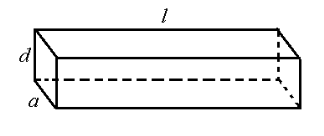
(1)在a>d>0的条件下,将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷会发生变化吗?变大还是变小?
(2)现有一根横截面为半圆(半圆的半径为R=![]() )的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
)的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com