
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,点
,点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,请问
,请问![]() 是否为定值?若是定值,求出其定值;若不是,说明理由.
是否为定值?若是定值,求出其定值;若不是,说明理由.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象是由函数![]() 的图象经如下变换得到:先将g(x)图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图象向右平移
的图象经如下变换得到:先将g(x)图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图象向右平移![]() 个单位长度.
个单位长度.
(1)求函数f(x)的解析式,并求其图象的对称轴方程;
(2)已知关于x的方程f(x)+g(x)=m在![]() 内有两个不同的解
内有两个不同的解![]() .
.
①求实数m的取值范围;
②证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 中,(底面为正三角形,侧棱垂直于底面),侧棱长
中,(底面为正三角形,侧棱垂直于底面),侧棱长![]() ,底面边长
,底面边长![]() ,
,![]() 是
是![]() 的中点.
的中点.
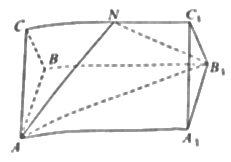
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学文化的优秀遗产,数学家刘徽在注解《九章算术》时,发现当圆内接正多边行的边数无限增加时,多边形的面积可无限逼近圆的面积,为此他创立了割圆术,利用割圆术,刘徽得到了圆周率精确到小数点后四位3.1416,后人称3.14为徽率,如图是利用刘徽的割圆术设计的程序框图,若结束程序时,则输出的![]() 为( )(
为( )(![]() ,
,![]() ,
,![]() )
)
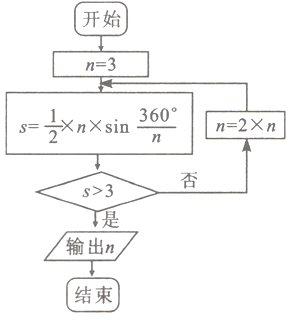
A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com