
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程是
的方程是![]() ,将
,将![]() 向上平移2个单位得到曲线
向上平移2个单位得到曲线![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为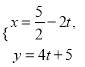 (
(![]() 为参数),判断直线
为参数),判断直线![]() 与曲线
与曲线![]() 的位置关系.
的位置关系.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程是
的方程是![]() ,将
,将![]() 向上平移2个单位得到曲线
向上平移2个单位得到曲线![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为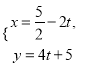 (
(![]() 为参数),判断直线
为参数),判断直线![]() 与曲线
与曲线![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个推理中,属于演绎推理的是( )
A. 观察下列各式:72=49,73=343,74=2401,…,则72015的末两位数字为43
B. 观察![]() ,可得偶函数的导函数为奇函数
,可得偶函数的导函数为奇函数
C. 在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4,类似的,在空间中,若两个正四面体的棱长比为1:2,则它们的体积之比为1:8
D. 已知碱金属都能与水发生还原反应,钠为碱金属,所以钠能与水发生反应
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示(单位:m),则该几何体的表面积为(单位:m2)( )
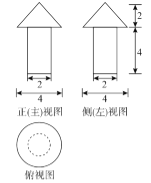
A. (11+4![]() )π B. (12+4
)π B. (12+4![]() )π C. (13+4
)π C. (13+4![]() )π D. (14+4
)π D. (14+4![]() )π
)π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点P到定点F(0,1)的距离比它到直线![]() 的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
(Ⅰ)求曲线C的方程;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)求△ABM的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,某城市的市民收入逐年增长,表1是该城市某银行连续五年的储蓄存款额(年底余额):
表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款额y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将表1的数据进行了处理,令t=x-2 010,z=y-5,得到表2:
表2
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)z关于t的线性回归方程是________;y关于x的线性回归方程是________;
(2)用所求回归方程预测到2020年年底,该银行储蓄存款额可达________千亿元.
(附:线性回归方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =
=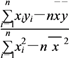 ,
,![]() =
=![]() -
-![]()
![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com