
【题目】某企业生产一种机器的固定成本(即固定投入)为 0.5 万元,但每生产100台时,又需可变成本(即另增加投入)0.25 万元.市场对此商品的年需求量为 500台,销售的收入(单位:万元)函数为 R(x)=5x-![]() x2(0≤x≤5),其中 x 是产品生产的数量(单位:百台).
x2(0≤x≤5),其中 x 是产品生产的数量(单位:百台).
(1)求利润关于产量的函数.
(2)年产量是多少时,企业所得的利润最大?
【答案】(1)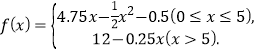 ;(2)475
;(2)475
【解析】
(1)由于商品年需求量为![]() ,故要对产量分成不大于
,故要对产量分成不大于![]() 和大于
和大于![]() 两段来求利润.当
两段来求利润.当![]() 时,用收入减掉成本,即为利润的值.当
时,用收入减掉成本,即为利润的值.当![]() 时,成本和
时,成本和![]() 的表达式一样,但是销售收入是固定的,由此求得解析式.(2)两段函数,二次函数部分用对称轴求得其最大值,一次函数部分由于是递减的,在左端点有最值的上限.比较两段函数的最大值,来求得整个函数的最大值.
的表达式一样,但是销售收入是固定的,由此求得解析式.(2)两段函数,二次函数部分用对称轴求得其最大值,一次函数部分由于是递减的,在左端点有最值的上限.比较两段函数的最大值,来求得整个函数的最大值.
(1)当 0≤x≤5 时,产品能全部售出,
则成本为 0.25x+0.5,收入为 5x-![]() x2,
x2,
利润 f(x)=5x-![]() x2-0.25x-0.5
x2-0.25x-0.5
=-![]() x2+4.75x-0.5.
x2+4.75x-0.5.
当 x>5 时,只能销售 500台,
则成本为 0.25x+0.5,销售收入为 5×5-![]() ×52=
×52=![]() ,
,
利润 f(x)=![]() -0.25x-0.5=-0.25x+12.
-0.25x-0.5=-0.25x+12.
综上,利润函数 f(x)=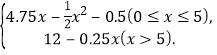
(2)当 0≤x≤5时,f(x)=-![]() (x-4.75)2+10.781 25,
(x-4.75)2+10.781 25,
当 x=4.75∈[0,5]时,f(x)max=10.781 25(万元);
当 x>5 时,函数 f(x) 是递减函数,则 f(x)<12-0.25×5=10.75(万元).
10.75<10.781 25.
综上,当年产量是 475台时,利润最大.


科目:高中数学 来源: 题型:
【题目】最新公布的《道路交通安全法》和《道路交通安全法实施条例》对车速、安全车距以及影响驾驶人反应快慢等因素均有详细规定,这些规定说到底主要与刹车距离有关,刹车距离是指从驾驶员发现障碍到制动车辆,最后完全停止所行驶的距离,即:刹车距离=反应距离+制动距离,反应距离=反应时间×速率,制动距离与速率的平方成正比,某反应时间为![]() 的驾驶员以
的驾驶员以![]() 的速率行驶,遇紧急情况,汽车的刹车距离为
的速率行驶,遇紧急情况,汽车的刹车距离为![]() .
.
(![]() )试将刹车距离
)试将刹车距离![]() 表示为速率
表示为速率![]() 的函数.
的函数.
(![]() )若该驾驶员驾驶汽车在限速为
)若该驾驶员驾驶汽车在限速为![]() 的公路上行驶,遇紧急情况,汽车的刹车距离为
的公路上行驶,遇紧急情况,汽车的刹车距离为![]() ,试问该车是否超速?请说明理由.
,试问该车是否超速?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
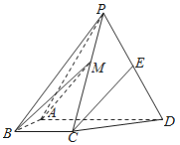
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点.
中点.
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)确定y=g(x),y=f(x)的解析式;
(2)若h(x)=f(x)+a在(﹣1,1)上有零点,求a的取值范围;
(3)若对任意的t∈(﹣4,4),不等式f(6t﹣3)+f(t2﹣k)<0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
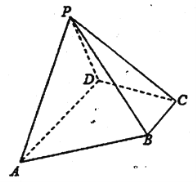
(1)求证:![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|.
(1)解不等式:f(x+1)+f(x+2)<4;
(2)已知a>2,求证:x∈R,f(ax)+af(x)>2恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面![]()
![]() 平面
平面![]() ,
, ![]() 与
与![]() 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形, ![]() //
// ![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() //
// ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的重心,
的重心, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() //平面
//平面![]() ;
;
(Ⅱ)若直线![]() 与
与![]() 所成角为
所成角为![]() ,试求二面角
,试求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知![]() 且
且![]() 设
设![]() ,绿地面积为
,绿地面积为![]() .
.
(1)写出![]() 关于
关于![]() 的函数关系式,并指出这个函数的定义域.
的函数关系式,并指出这个函数的定义域.
(2)当![]() 为何值时,绿地面积
为何值时,绿地面积![]() 最大?
最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com