
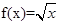 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.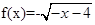 .
. .由函数f(x)的图象关于直线
.由函数f(x)的图象关于直线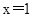 对称,可得
对称,可得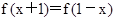 ,
,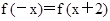 .根据函数
.根据函数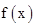 是定义在R上的奇函数,故有
是定义在R上的奇函数,故有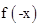 =-
=-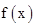 .
.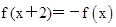 ,得到
,得到 ,即f(x)是周期为4的周期函数.
,即f(x)是周期为4的周期函数.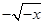 .
. 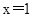 对称,有
对称,有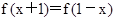 ,
,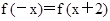 2分
2分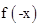 =-
=-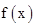 .
.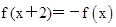 ,从而
,从而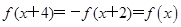 ,即
,即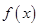 是周期为4的周期函数. 6分
是周期为4的周期函数. 6分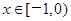 时,
时,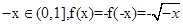 .
. 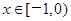 时,
时,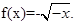 9分
9分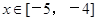 时,
时,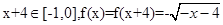 .
.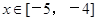 时,函数f(x)的解析式为
时,函数f(x)的解析式为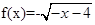 . 12分
. 12分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 和分别以
和分别以 、
、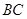 为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,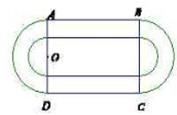
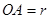 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积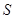 与
与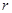 的函数关系式
的函数关系式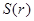 ;
;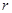 的范围为
的范围为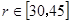 ,问当
,问当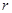 为何值时,运动场造价最低(第2问
为何值时,运动场造价最低(第2问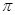 取3近似计算).
取3近似计算).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的定义域为
的定义域为 ,部分对应值如表.
,部分对应值如表. 的导函数
的导函数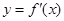 的图象如图所示.下列关于函数
的图象如图所示.下列关于函数 的命题:①函数
的命题:①函数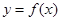 是周期函数;②函数
是周期函数;②函数 在
在 是减函数;③如果当
是减函数;③如果当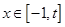 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;④当
的最大值为4;④当 时,函数
时,函数 有4个零点.其中真命题的个数是 .
有4个零点.其中真命题的个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com