
【题目】关于x方程 ![]() ﹣x=lnx有唯一的解,则实数a的取值范围是 .
﹣x=lnx有唯一的解,则实数a的取值范围是 .
【答案】{a|a<0或a=1}
【解析】解:要使方程有意义,则x>0,
设f(x)= ![]() ﹣x,g(x)=lnx,
﹣x,g(x)=lnx,
若a<0,此时函数f(x)在x>0时,单调递减,g(x)=lnx单调递增,
此时两个函数只有一个交点,满足方程有唯一解;
若a>0,要使方程 ![]() ﹣x=lnx有唯一的解,
﹣x=lnx有唯一的解,
则函数f(x)与g(x)有相同的切线,
设切点为(m,n),
则f′(x)= ![]() ,g′(x)=
,g′(x)= ![]() ,
,
则满足 ![]() ﹣1=
﹣1= ![]() ,
,
即 ![]() ﹣m=1①,
﹣m=1①,
同时 ![]() ﹣m=lnm,②
﹣m=lnm,②
①﹣2×②得m=1﹣2lnm,
即m﹣1=﹣2lnm,
∵y=m﹣1与y=﹣2lnm只有一个根,
∴解得m=1,
当m=1时,n=ln1=0,
即切点为(1,0),
则f(x)与g(x)在(1,0)处相切,
即此时f(1)=0,即a=1,满足条件.
所以答案是:{a|a<0或a=1}



 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】函数y= ![]() cos(
cos( ![]() ﹣2x)的单调递增区间是( )
﹣2x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ﹣ ![]() ,kπ)(k∈Z)
,kπ)(k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ+ ![]() ,kπ+π](k∈Z)
,kπ+π](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣(a+1)lnx﹣ ![]() ,其中a∈R.
,其中a∈R.
(Ⅰ)求证:当a=1时,函数y=f(x)没有极值点;
(Ⅱ)求函数y=f(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
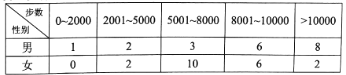
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?

附:  ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an},a1=1,an=an+12+2an+1(Ⅰ)求证:数列{log2(an+1)}为等比数列:
(Ⅱ)设bn=n1og2(an+1),数列{bn}的前n项和为Sn , 求证:1≤Sn<4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com