
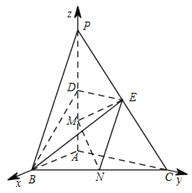
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC, ![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C-EM-N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.

【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]() .
.
【解析】试题分析:本小题主要考查直线与平面平行、二面角、异面直线所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.首先要建立空间直角坐标系,写出相关点的坐标,证明线面平行只需求出平面的法向量,计算直线对应的向量与法向量的数量积为0,求二面角只需求出两个半平面对应的法向量,借助法向量的夹角求二面角,利用向量的夹角公式,求出异面直线所成角的余弦值,利用已知条件,求出![]() 的值.
的值.
试题解析:如图,以A为原点,分别以![]() ,
, ![]() ,
, ![]() 方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A(0,0,0),B(2,0,0),C(0,4,0),P(0,0,4),D(0,0,2),E(0,2,2),M(0,0,1),N(1,2,0).
方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A(0,0,0),B(2,0,0),C(0,4,0),P(0,0,4),D(0,0,2),E(0,2,2),M(0,0,1),N(1,2,0).
(Ⅰ)证明: ![]() =(0,2,0),
=(0,2,0),![]() =(2,0,
=(2,0, ![]() ).设
).设![]() ,为平面BDE的法向量,
,为平面BDE的法向量,
则![]() ,即
,即![]() .不妨设
.不妨设![]() ,可得
,可得![]() .又
.又![]() =(1,2,
=(1,2, ![]() ),可得
),可得![]() .
.
因为![]() 平面BDE,所以MN//平面BDE.
平面BDE,所以MN//平面BDE.
(Ⅱ)解:易知![]() 为平面CEM的一个法向量.设
为平面CEM的一个法向量.设![]() 为平面EMN的法向量,则
为平面EMN的法向量,则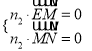 ,因为
,因为![]() ,
, ![]() ,所以
,所以![]() .不妨设
.不妨设![]() ,可得
,可得![]() .
.
因此有![]() ,于是
,于是![]() .
.
所以,二面角C—EM—N的正弦值为![]() .
.
(Ⅲ)解:依题意,设AH=h(![]() ),则H(0,0,h),进而可得
),则H(0,0,h),进而可得![]() ,
, ![]() .由已知,得
.由已知,得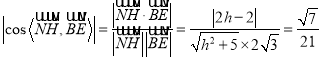 ,整理得
,整理得![]() ,解得
,解得![]() ,或
,或![]() .
.
所以,线段AH的长为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(﹣2,0),点B(2, ![]() )在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
)在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点P,使得无论非零实数k怎样变化,总有∠MPN为直角?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() ,cos
,cos ![]() ),
), ![]() =(cos
=(cos ![]() ,1),且f(x)=
,1),且f(x)= ![]()
![]() .
.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[﹣π,π]上的最大值和最小值及取得最值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量 ![]() ,
, ![]() (
( ![]() ≠
≠ ![]() )满足
)满足 ![]() =2,且
=2,且 ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为120° , t∈R,则|(1﹣t)
的夹角为120° , t∈R,则|(1﹣t) ![]() +t
+t ![]() |的最小值是 . 已知
|的最小值是 . 已知 ![]()
![]() =0,向量
=0,向量 ![]() 满足(
满足( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,|
)=0,| ![]() ﹣
﹣ ![]() |=5,|
|=5,| ![]() ﹣
﹣ ![]() |=3,则
|=3,则 ![]()
![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
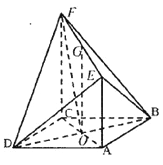
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)当直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 倾斜角是
倾斜角是![]() 且过抛物线
且过抛物线![]() 的焦点,直线
的焦点,直线![]() 被抛物线
被抛物线![]() 截得的线段长是16,双曲线
截得的线段长是16,双曲线![]() :
: ![]() 的一个焦点在抛物线
的一个焦点在抛物线![]() 的准线上,则直线
的准线上,则直线![]() 与
与![]() 轴的交点
轴的交点![]() 到双曲线
到双曲线![]() 的一条渐近线的距离是( )
的一条渐近线的距离是( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com