
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() ,与
,与![]() ,
,![]() 各有一个交点,当
各有一个交点,当![]() 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当![]() ,这两个交点重合.
,这两个交点重合.
(1)分别说明![]() ,
,![]() 是什么曲线,并求出
是什么曲线,并求出![]() 与
与![]() 的值;
的值;
(2)设当![]() 时,
时,![]() 与
与![]() ,
,![]() 的交点分别为
的交点分别为![]() ,当
,当![]() ,
,![]() 与
与![]() ,
,![]() 的交点分别为
的交点分别为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据四川省民政厅报告,2013年6月29日以来,四川省中东部出现强降雨天气过程,局地出现大暴雨.暴雨洪涝灾害已造成遂宁、德阳、绵阳等12市34县(市、区)244万人受灾,共造成直接经济损失85502.41万元.适逢暑假,小王在某小区调查了50户居民由于洪灾造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图(如图).
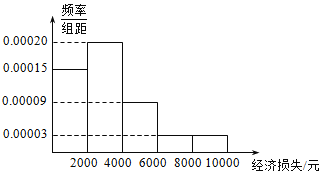
(1)若先从损失超过6000元的居民中随机抽出2户进行调查,求这2户不在同一小组的概率;(2)洪灾过后小区居委会号召小区居民为洪灾重灾区捐款,小王调查的50户居民的捐款情况如表,在表格空白处填写正确的数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?

P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:临界值表参考公式:K2=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.
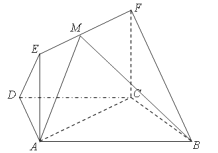
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,将四边形
,将四边形![]() 沿
沿![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上.
上.
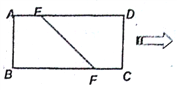
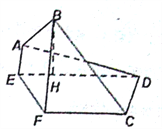
(I)求证: ![]() ;
;
(II)求点![]() 到平面
到平面![]() 的距离;
的距离;
(III)求直线![]() 与平面
与平面![]() 所成的正弦值.
所成的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯
为梯
形, ![]() ,
, ![]() ,
, ![]() .且
.且![]() 与
与![]() 均为正三角形,
均为正三角形, ![]() 为
为![]() 的中点,
的中点,
![]() 为
为![]() 重心.
重心.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届广东省深圳市高三下学期第一次调研考试(一模)数学理】已知函数![]() 为自然对数的底数.
为自然对数的底数.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的值;
的值;
(3)关于![]() 的方程
的方程![]() 有两个实根
有两个实根![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司做了一次抽样调查,并统计得出某款车的使用年限![]() (单位:年)与所支出的总费用
(单位:年)与所支出的总费用![]() (单位:万元)有如下的数据资料:
(单位:万元)有如下的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知![]() 对
对![]() 呈线性相关关系.
呈线性相关关系.
(1)试求线性回归方程![]() =
=![]()
![]() +
+![]() 的回归系数
的回归系数![]() ,
,![]() ;
;
(2)当使用年限为![]() 年时,估计车的使用总费用.
年时,估计车的使用总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com