
分析 (1)利用奇函数的定义,即可证明;
(2)利用导数大于0,即可证明.
解答 证明:(1)函数的定义域为R,
∴f(x)=$\frac{{2}^{x}-1}{2({2}^{x}+1)}$
∴f(-x)=$\frac{{2}^{-x}-1}{2({2}^{-x}+1)}$=-$\frac{{2}^{x}-1}{2({2}^{x}+1)}$=-f(x),
∴函数f(x)是奇函数;
(2)∵f(x)=$\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$
∴f′(x)=-$\frac{{-2}^{x}ln2}{({2}^{x}+1)^{2}}$>0
∴函数f(x)在R上是增函数.
点评 本题考查函数的单调性、奇偶性,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3π}{16}$,0) | B. | ($\frac{3π}{16}$,0) | C. | ($\frac{7π}{16}$,0) | D. | ($\frac{15π}{16}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
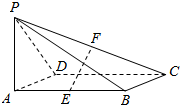 如图,已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD=1,AB=$\sqrt{2}$,点E,F分别为AB、PC中点.
如图,已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD=1,AB=$\sqrt{2}$,点E,F分别为AB、PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
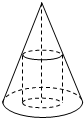 如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.
如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤-1} | B. | {x|-2≤x≤-1或x=0} | C. | {x|-2≤x<-1} | D. | {x|-2≤x<-1或x=0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (1,2] | C. | [2,3) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com