
分析 (1)根据对数函数的性质求出a的值即可;
(2)根据对数函数的性质得到关于x的不等式组,解出即可;
(3)求出g(x)的分段函数的形式,从而求出函数的单调区即可.
解答 解:(1)∵loga3>loga2,∴a>1,
又∵y=logax在[a,2a]上为增函数,
∴loga2a-logaa=1,即loga2=1,∴a=2.
(2)依题意可知$\left\{\begin{array}{l}x-1<2-x\\ x-1>0\end{array}\right.$
解得$1<x<\frac{3}{2}$,∴所求不等式的解集为$({1,\frac{3}{2}})$.
(3)∵g(x)=|log2x-1|,∴g(x)≥0,当且仅当x=2时,g(x)=0.
则$g(x)=\left\{\begin{array}{l}1-{log_2}x,0<x≤2\\{log_2}x-1,x>2\end{array}\right.$
∴函数在(0,2)上为减函数,在(2,+∞)上为增函数,
g(x)的减区间为(0,2),增区间为(2,+∞).
点评 本题考查了函数的单调性问题,考查对数函数的性质,是一道中档题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2${\;}^{\sqrt{3}-1}$-2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,+∞),lnx≠x-1 | B. | ?x∉(0,+∞),lnx=x-1 | ||
| C. | ?x0∈(0,+∞),lnx0≠x0-1 | D. | ?x0∉(0,+∞),lnx0=x0-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
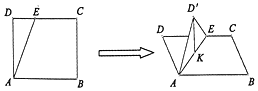 如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )
如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | $(\root{3}{3},2)$ | C. | $(\root{3}{4},2)$ | D. | $(\root{3}{2},3)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2=1 | B. | x2+y2=16 | C. | x2+y2=9 | D. | x2+y2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com