Question

在区间[0，1]上任取两个数a，b，方程x²+ax+b²=0的两根均为实数的概率为

0.25

．

Answer 1

分析：方程x²+ax+b²=0的两根均为实数，则△=a²-4b²≥0，利用a，b是区间[0，1]上任取的两个数，以面积为测度，可求得结论．

解答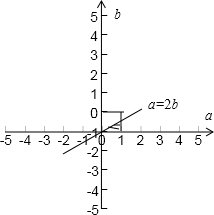：解：∵方程x²+ax+b²=0的两根均为实数，∴△=a²-4b²≥0，
∵a，b是区间[0，1]上任取的两个数，∴a≥2b
建立平面直角坐标系，两坐标轴分别为a轴，b轴，不等式表示a=2b的下方区域，
其面积为

1

2

×1×

1

2

=0.25
∵正方形区域的面积为1
∴方程x²+ax+b²=0的两根均为实数的概率为0.25
故答案为：0.25．

点评：本题考查几何概型，考查数形结合的数学思想，属于基础题．