练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．设等差数列{an}的前n项和为Sn，若Sm-2=-4，Sm=0，Sm+2=12，则第m项am=（　　）
    A．0B．1C．3D．8

    分析 根据等差数列的通项公式和前n项和公式，建立方程，即可得出结论．

    解答 解：∵等差数列{an}的前n项和为Sn，Sm-2=-4，Sm=0，Sm+2=12，
    ∴am+am-1=Sm-Sm-2=0+4=4，
    am+2+am+1=Sm+2-Sm=12-0=12，
    即$\left\{\begin{array}{l}{{a}_{1}+（m-1）d+{a}_{1}+（m-2）d=2}\\{{a}_{1}+（m+1）d+{a}_{1}+md=12}\end{array}\right.$，
    解得d=2，
    ∴am=$\frac{1}{2}$（am+am-1+d）=$\frac{1}{2}$（4+2）=3．
    故选：C．

    点评 本题考查等差数列的第m项的求法，是中档题，解题时要认真审题，注意等差数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．已知n=9$\int_{-1}^1{x^2}$dx，在二项式${（x-\frac{2}{x}）^n}$的展开式中，x2的系数是60．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知sin（$\frac{π}{6}$+α）=$\frac{1}{3}$，则cos（$\frac{2π}{3}$-2α）=（　　）
    A．$\frac{4\sqrt{2}}{9}$B．$\frac{8}{9}$C．-$\frac{7}{9}$D．$\frac{7}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

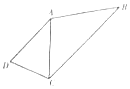    10．如图，四边形ABCD中，AD∥BC，∠DAC=45°，∠ADC=60°，DC=$\sqrt{6}$，AB=3$\sqrt{2}$．
    （1）求AC的长；
    （2）求∠ABC的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知△ABC中，角A，B，C所对的边分别是a，b，c，$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{b}$+2$\sqrt{3}$csinA=2b+4c，且14sinC=3$\sqrt{3}$．
    （1）求A的大小；
    （2）若c=3，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知函数f（x）=x-1-lnx，对定义域内任意x都有f（x）≥kx-2，则实数k的取值范围是（　　）
    A．（-∞，1-$\frac{1}{{e}^{2}}$]B．（-∞，-$\frac{1}{{e}^{2}}$]C．[-$\frac{1}{{e}^{2}}$，+∞）D．[1-$\frac{1}{{e}^{2}}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=|x+1|+|x-2|，f（x）-m≥0恒成立．
    （1）求实数m的取值范围；
    （2）m的最大值为n，解不等式|x-3|-2x≤n+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知指数函数y=g（x）的图象经过点（2，4），且定义域为R的函数f（x）=$\frac{b-g（x）}{a+g（x）}$是奇函数．
    （1）求f（x）的解析式，判断f（x）在定义域R上的单调性，并给予证明；
    （2）若关于x的方程f（x）=m在[-1，0）上有解，求f（$\frac{1}{m}$）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知数列{an}中，a1=4，an=an-1+2n-1+3（n≥2，n∈N*）．
    （Ⅰ）证明数{an-2n}是等差数列，并求{an}的通项公式；
    （Ⅱ）设bn=an-3n，求bn的前n项和Tn．

    查看答案和解析>>

    同步练习册答案