
【题目】设函数![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)当![]() 时,证明:
时,证明:![]() 在
在![]() 上恒成立.
上恒成立.
【答案】(1)![]() 在
在![]() 处取得极大值
处取得极大值![]() 无极小值(2)详见解析
无极小值(2)详见解析
【解析】
试题分析:(1)先求导数![]() ,再求导函数在定义区间上的零点
,再求导函数在定义区间上的零点![]() ,列表分析函数单调性变化趋势,确定极值(2)证明不等式,一般利用函数最值进行证明,而构造恰当的函数是解题的关键与难点,因为
,列表分析函数单调性变化趋势,确定极值(2)证明不等式,一般利用函数最值进行证明,而构造恰当的函数是解题的关键与难点,因为![]() ,所以首先将对数函数与指数函数分离,为使函数有最值,再作变形:
,所以首先将对数函数与指数函数分离,为使函数有最值,再作变形:![]() ,这样只需证明:
,这样只需证明:![]() ,利用导数不难求得
,利用导数不难求得![]() ,
,![]() ,所以
,所以![]() ,但等号取法不同,因此
,但等号取法不同,因此![]()
试题解析:(1)当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴![]() 在
在![]() 处取得极大值
处取得极大值![]() 无极小值
无极小值
(2)当![]() 时,
时,![]() ,
,
下面证![]() ,即证
,即证![]() .
.
设![]() , 则
, 则![]() ,
,
在![]() 上,
上,![]() 是减函数;在
是减函数;在![]() 上,
上,![]() 是增函数.
是增函数.
所以![]() .
.
设![]() , 则
, 则![]() ,
,
在![]() 上,
上,![]() 是增函数;在
是增函数;在![]() 上,
上,![]() 是减函数,
是减函数,
所以![]() ,.
,.
所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,
,
即![]() 在
在![]() 上恒成立
上恒成立


科目:高中数学 来源: 题型:
【题目】探索表达式A=(n-1)(n-1)!+(n-2)(n-2)!+…+2·2!+1·1!(n>1,且n∈N*)的结果时,第一步当n=____时,A=____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间,生物、数学、物理、化学四项大赛在北京、重庆、石家庄、天津举行.我校学生张丽、马灵、赵明、陆俊参赛,每人只报不同的一项.已知张丽在北京比赛,生物在重庆举行,马灵在石家庄比赛,陆俊参加数学比赛,张丽没有参加化学比赛,则下列判断正确的是( )
A. 张丽在北京参加数学比赛 B. 赵明在重庆参加生物比赛
C. 马灵在石家庄参加物理比赛 D. 陆俊在天津参加化学比赛
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射手射击所得环数ξ的分布列如下:
ξ | 7 | 8 | 9 | 10 |
P | x | 0.1 | 0.3 | y |
已知ξ的数学期望E(ξ)=8.9,则y的值为( ).
A. 0.2 B. 0.4 C. 0.6 D. 0.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个侧棱长为![]() 的直三棱柱
的直三棱柱![]() 容器中盛有液体(不计容器厚度).若液面恰好分别过棱
容器中盛有液体(不计容器厚度).若液面恰好分别过棱![]() 中点
中点![]() .
.
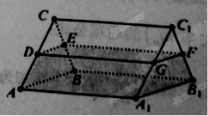
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当底面![]() 水平放置时,求液面的高.
水平放置时,求液面的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于①“一定发生的”,②“很可能发生的”,③“可能发生的”,④“不可能发生的”,⑤“不太可能发生的”这5种生活现象,发生的概率由小到大排列为(填序号)_________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com