
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.

(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为
的回归方程,并预测液体肥料每亩使用量为![]() 千克时,西红柿亩产量的增加量约为多少?
千克时,西红柿亩产量的增加量约为多少?
附:相关系数公式 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() 和⊙
和⊙![]()
![]() ,过抛线
,过抛线![]() 上一点
上一点![]() 作两条直线与⊙
作两条直线与⊙![]() 相切于A、B两点,分别交抛物线于E、F两点,圆心点
相切于A、B两点,分别交抛物线于E、F两点,圆心点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() .
.
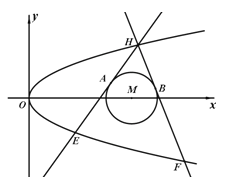
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)当![]() 的角平分线垂直x轴时,求直线EF的斜率;
的角平分线垂直x轴时,求直线EF的斜率;
(Ⅲ)若直线AB在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是正整数.在一个十进制
是正整数.在一个十进制![]() 位数的各位数字中,若含有数字8,则在每个数字8的前一位数字就不能是数字3(即不能出现38字样).试求出所有这样的
位数的各位数字中,若含有数字8,则在每个数字8的前一位数字就不能是数字3(即不能出现38字样).试求出所有这样的![]() 位数的个数.
位数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄X分别为16岁、18岁、20岁和22岁者,其得肺癌的相对危险度Y依次为15.10,12.81,9.72,3.21;每天吸烟支数U分别为10,20,30者,其得肺癌的相对危险度V分别为7.5,9.5和16.6,用![]() 表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
A.r1=r2B.r1>r2>0
C.0<r1<r2D.r1<0<r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知圆C的圆心![]() ,半径r=3.
,半径r=3.
(1)求圆C的极坐标方程;
(2)若Q点在圆C上运动,P在OQ的延长线上,且![]() ,求动点P的轨迹的极坐标方程.
,求动点P的轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() 得到如图所示的频率分布直方图.
得到如图所示的频率分布直方图.
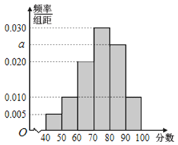
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请在答题卡上将![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
参考公式及数据: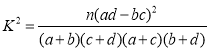 ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为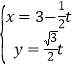 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,记弦
两点,记弦![]() 的中点为
的中点为![]() ,点
,点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
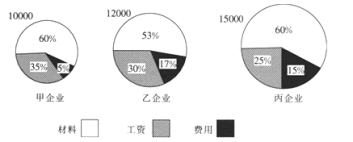
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com