
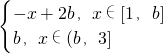 ,1<b<3.g(x)=f(x)+ax,x∈[1,3].
,1<b<3.g(x)=f(x)+ax,x∈[1,3]. ,(2分)
,(2分) ,∴a<0(4分)
,∴a<0(4分)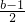 时,max{g(x)|x∈[1,3]}=g(1)=a+2b-1,min{g(x)|x∈[1,3]}=g(b)=ab+b,此时,h(a)=a+b-ab-1
时,max{g(x)|x∈[1,3]}=g(1)=a+2b-1,min{g(x)|x∈[1,3]}=g(b)=ab+b,此时,h(a)=a+b-ab-1 时,max{g(x)|x∈[1,3]}=g(3)=3a+b,min{g(x)|x∈[1,3]}=g(b)=ab+b,此时,h(a)=3a-ab,故h(a)=
时,max{g(x)|x∈[1,3]}=g(3)=3a+b,min{g(x)|x∈[1,3]}=g(b)=ab+b,此时,h(a)=3a-ab,故h(a)= ,(2分)
,(2分)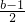 ]上单调递减,在[
]上单调递减,在[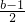 ,1]单调递增,故d(b)=min{h(a)|a∈R}=h(
,1]单调递增,故d(b)=min{h(a)|a∈R}=h(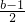 )=
)= ,(4分)
,(4分) . (6分)
. (6分) ,即x=b时,g[f(x)]=ab+b
,即x=b时,g[f(x)]=ab+b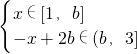 时,即
时,即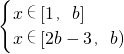 (*),(3分)
(*),(3分)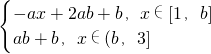
 (7分)
(7分)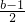 ,
, ,分别求出max{g(x)|x∈[1,3]}与min{g(x)|x∈[1,3]},即可求得h(a)的表达式,利用函数的单调性,可求出min{d(b)|b∈(1,3)};
,分别求出max{g(x)|x∈[1,3]}与min{g(x)|x∈[1,3]},即可求得h(a)的表达式,利用函数的单调性,可求出min{d(b)|b∈(1,3)}; ,即x=b时,g[f(x)]=ab+b
,即x=b时,g[f(x)]=ab+b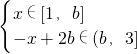 时,即
时,即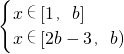 ,g[f(x)]=
,g[f(x)]=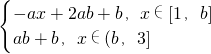 ,由此可得k(a)的表达式,从而可求min{k(a)|a∈R}.
,由此可得k(a)的表达式,从而可求min{k(a)|a∈R}.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| b-1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2012年上海市闵行区高考数学一模试卷(文科)(解析版) 题型:解答题
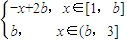 (1<b<3),g(x)=f(x)+ax,x∈[1,3],令h(a)=max{g(x)|x∈[1,3]}-min{g(x)|x∈[1,3]},记d(b)=min{h(a)|a∈R}.
(1<b<3),g(x)=f(x)+ax,x∈[1,3],令h(a)=max{g(x)|x∈[1,3]}-min{g(x)|x∈[1,3]},记d(b)=min{h(a)|a∈R}.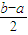 时,求h(a)关于a的表达式;
时,求h(a)关于a的表达式;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com