抛物线绕轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是．题目和参考答案——青夏教育精英家教网—

抛物线绕轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是．

【答案】

【解析】

试题分析：根据旋转体的对称性，不妨设正方体的一个对角面恰好在平面内，组合体被此面所截得的截面图如下：

设正方体的棱长为，则，，

因为，所以，，即：

解得：或，因为，所以.

考点：1、抛物线标准方程的应用；2、正方体的结构特征.

练习册系列答案

思维新观察同步检测金卷系列答案

相关习题

科目：高中数学 来源： 题型：

（2012•黄浦区二模）已知三棱锥P-ABC，PA⊥平面ABC，AB⊥AC，AB=AC=4，AP=5．
（1）求二面角P-BC-A的大小（结果用反三角函数值表示）．
（2）把△PAB（及其内部）绕PA所在直线旋转一周形成一几何体，求该几何体的体积V．

科目：高中数学 来源： 题型：

（2012•浦东新区三模）如图，弧AEC是半径为r的半圆，AC为直径，点E为弧AC的中点，点B和点C为线段AD的三等分点，线段ED与弧EC交于点G，且EG=

GD，平面AEC外一点F满足FC⊥平面BED，FC=2r．
（1）证明：EB⊥FD；
（2）将△FCG（及其内部）绕FC所在直线旋转一周形成一几何体，求该几何体的体积．

科目：高中数学 来源： 题型：

（2012•浦东新区三模）如图，弧AEC是半径为r的半圆，AC为直径，点E为弧AC的中点，点B和点C为线段AD的三等分点，线段ED 与弧EC交于点G，且cos∠CBG=

，平面AEC外一点F满足FC⊥平面BED，FC=2r．
（1）求异面直线ED与FC所成角的大小；
（2）将△FCG（及其内部）绕FC所在直线旋转一周形成一几何体，求该几何体的体积．

科目：高中数学 来源：2013-2014学年安徽省六校教育研究会高三2月联考理科数学试卷（解析版） 题型：填空题

抛物线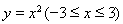绕轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是．

同步练习册答案