
【题目】如图分别为定义域和值域均为![]() 的函数
的函数![]() 和函数
和函数![]() 的图象,则下列命题正确的是( )
的图象,则下列命题正确的是( )
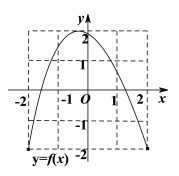
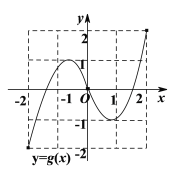
A.函数![]() 恰有
恰有![]() 个零点B.函数
个零点B.函数![]() 恰有
恰有![]() 个零点
个零点
C.函数![]() 恰有
恰有![]() 个零点D.函数
个零点D.函数![]() 恰有
恰有![]() 个零点
个零点
【答案】C
【解析】
将各选项中的复合函数分为内层函数和外层函数,先分析外层函数的零点及其范围,再分析内层函数方程的根的个数,即可得出结论.
对于A选项,令![]() ,
,
则外层函数![]() 有
有![]() 个零点
个零点![]() ,
,![]() ,
,
关于![]() 的方程
的方程![]() 只有1个根,关于
只有1个根,关于![]() 的方程
的方程![]() 只有1个根,
只有1个根,
所以,函数![]() 恰有
恰有![]() 个零点,A选项错误;
个零点,A选项错误;
对于B选项,令![]() ,
,
则外层函数![]() 有
有![]() 个零点
个零点![]() ,
,![]() ,
,![]() ,
,
关于![]() 的方程
的方程![]() 有
有![]() 个根,关于
个根,关于![]() 的方程
的方程![]() 有
有![]() 个根,关于
个根,关于![]() 的方程
的方程![]() 有
有![]() 个根,
个根,
所以,函数![]() 恰有
恰有![]() 个零点,B选项错误;
个零点,B选项错误;
对于C选项,令![]() ,
,
则外层函数![]() 有
有![]() 个零点
个零点![]() ,
,![]() ,
,
关于![]() 的方程
的方程![]() 有
有![]() 个根,关于
个根,关于![]() 的方程
的方程![]() 有
有![]() 个根,
个根,
所以,函数![]() 恰有
恰有![]() 个零点,C选项正确;
个零点,C选项正确;
对于D选项,令![]() ,
,
则外层函数![]() 有
有![]() 个零点
个零点![]() ,
,![]() ,
,![]() ,
,
关![]() 的方程
的方程![]() 有
有![]() 个根,关
个根,关![]() 的方程
的方程![]() 有3个根,关于
有3个根,关于![]() 的方程
的方程![]() 有1个根,
有1个根,
所以,函数![]() 恰有
恰有![]() 个零点.
个零点.
故选:C.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究在
两点,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得可
,使得可![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标,若不存在,请说明理由?
的坐标,若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个摸球游戏,规则如下:在一不透明的纸盒中,装有6个大小相同、颜色各异的玻璃球.参加者交费1元可玩1次游戏,从中有放回地摸球3次.参加者预先指定盒中的某一种颜色的玻璃球,然后摸球.当所指定的玻璃球不出现时,游戏费被没收;当所指定的玻璃球出现1次,2次,3次时,参加者可相应获得游戏费的0倍,1倍,![]() 倍的奖励(
倍的奖励(![]() ),且游戏费仍退还给参加者.记参加者玩1次游戏的收益为
),且游戏费仍退还给参加者.记参加者玩1次游戏的收益为![]() 元.
元.
(1)求概率![]() 的值;
的值;
(2)为使收益![]() 的数学期望不小于0元,求
的数学期望不小于0元,求![]() 的最小值.
的最小值.
(注:概率学源于赌博,请自觉远离不正当的游戏!)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)若函数![]() 在其定义域上为单调函数,求
在其定义域上为单调函数,求![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 的图像在
的图像在![]() 处的切线的斜率为0,
处的切线的斜率为0,![]() ,已知
,已知![]() 求证:
求证:![]()
(Ⅲ)在(2)的条件下,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校将甲、乙等6名新招聘的老师分配到4个不同的年级,每个年级至少分配1名教师,且甲、乙两名老师必须分到同一个年级,则不同的分法种数为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知i为虚数单位,a为实数,复数z=(1﹣2i)(a+i)在复平面内对应的点为M,则![]() “”是“点M在第四象限”的( )
“”是“点M在第四象限”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的圆心坐标为(1,0),半径为1.
(1)求圆C的极坐标方程;
(2)若以极点O为原点,极轴所在直线为x轴建立平面直角坐标系.已知直线l的参数方程为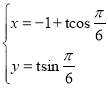 (t为参数),试判断直线l与圆C的位置关系.
(t为参数),试判断直线l与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生参加4门学科的学业水平测试,每门得![]() 等级的概率都是
等级的概率都是![]() ,该学生各学科等级成绩彼此独立.规定:有一门学科获
,该学生各学科等级成绩彼此独立.规定:有一门学科获![]() 等级加1分,有两门学科获
等级加1分,有两门学科获![]() 等级加2分,有三门学科获
等级加2分,有三门学科获![]() 等级加3分,四门学科全获
等级加3分,四门学科全获![]() 等级则加5分,记
等级则加5分,记![]() 表示该生的加分数,
表示该生的加分数, ![]() 表示该生获
表示该生获![]() 等级的学科门数与未获
等级的学科门数与未获![]() 等级学科门数的差的绝对值.
等级学科门数的差的绝对值.
(1)求![]() 的数学期望;
的数学期望;
(2)求![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com