
分析 若存在λ∈R,使$\overrightarrow{a}$=λ$\overrightarrow{b}$,则l1与l2平行;若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则l1与l2垂直,进而可得结论.
解答 解:①∵$\overrightarrow{a}$=(4,6,-2),$\overrightarrow{b}$=(-2,-3,1),
∴$\overrightarrow{a}$=-2$\overrightarrow{b}$,
∴l1∥l2;
②∵$\overrightarrow{a}$=(5,0,2),$\overrightarrow{b}$=(0,1,0),
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴l1⊥l2;
③∵$\overrightarrow{a}$=(-2,-1,-1),$\overrightarrow{b}$=(4,-2,-8).
∴不存在λ∈R,使$\overrightarrow{a}$=λ$\overrightarrow{b}$,
故l1与l2不平行,
且$\overrightarrow{a}$•$\overrightarrow{b}$=2≠0,
故l1与l2不垂直,
故l1与l2不平行与不垂直;
点评 本题考查的知识点是直线的方向向量,直线与直线位置关系的判断,难度不大,属于基础题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
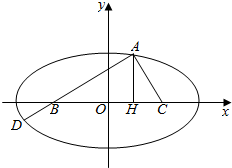 如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.
如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com