
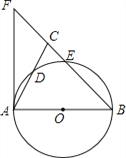
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若![]() ,CE∶EB=1∶4,求CE的长.
,CE∶EB=1∶4,求CE的长.
【答案】(1)见解析;(2)2。
【解析】试题分析:(1)依据题设条件证明“∠CAF=∠ABD”,即说明BA=BC,再借助等腰三角形的高线即为角平分线进行推证;(2)借助相似三角形的性质,即对应边成比例建立方程进行求解:
解: (1) 证明:连接BD.
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°.
∵AF是⊙O的切线,
∴∠FAB=90°,
∴∠CAF+∠DAB=90°,
∴∠CAF=∠ABD,
∴BA=BC
∴∠ABC=2∠ABD
∴∠ABC=2∠CAF.
(2)解:连接DE,
∵四边形ABED是圆内接四边形,
∴∠ABC=∠CDE,∠CED=∠CAB,
∴△CDE∽△CBA,
∴CD∶CB=CE∶CA
∴CD×CA=CE×CB
∴BA=BC,∠ADB=90°
∴![]()
设CE=x,∵CE:EB=1:4,∴EB=5x,
∴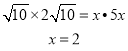
∴CE=2.


科目:高中数学 来源: 题型:
【题目】如图,已知底角为45的等腰梯形ABCD,底边BC长为7cm,腰长为![]() ,当一条垂直于底边BC
,当一条垂直于底边BC
(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x
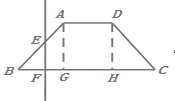
(1)试写出直线l左边部分的面积f(x)与x的函数.
(2)已知A={x|f(x)<4},B={x|a2<x<a+2},若A∪B=B,求a的取值范围。.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)若![]() 的图象在
的图象在![]() 处的切线恰好也是
处的切线恰好也是![]() 图象的切线.
图象的切线.
①求实数![]() 的值;
的值;
②若方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围.
的取值范围.
(2)当![]() 时,求证:对于区间
时,求证:对于区间![]() 上的任意两个不相等的实数
上的任意两个不相等的实数![]() ,
, ![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos xsin 2x,下列结论中正确的是________(填入正确结论的序号).
①y=f(x)的图象关于点(2π,0)中心对称;
②y=f(x)的图象关于直线x=π对称;
③f(x)的最大值为![]() ;
;
④f(x)既是奇函数,又是周期函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题13分)已知函数f(x)=![]() -
-![]() (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在[![]() ,2]上的值域是[
,2]上的值域是[![]() ,2],求a的值.
,2],求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: ![]() ,
, ![]() ,
, ![]() ,…
,…![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
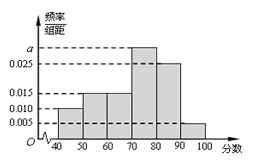
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(2)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是R上的偶函数,且当x>0时,函数的解析式为f(x)=![]() .
.
(1)判断并证明f(x)在(0,+∞)上的单调性;
(2)求当x<0时,函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com