
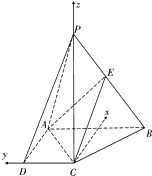
【题目】如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点. 
(1)求证:CE∥平面PAD;
(2)若二面角P﹣AC﹣E的余弦值为 ![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
【答案】
(1)证明:取线段AB的中点F,连接EF,CF.则AF=CD,AF∥CD,
所以四边形ADCF是平行四边形,
则CF∥AD;
又EF∥AP且CF∩EF=F,
∴面CFE∥面PAD,
又EC面CEF,
∴EC∥平面PAD

(2)解:如图,以C为原点,取AB中点F, ![]() 、
、 ![]() 、
、 ![]() 分别为x轴、y轴、z轴正向,
分别为x轴、y轴、z轴正向,
建立空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,﹣1,0).
设P(0,0,a)(a>0),则E( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
),
![]() =(1,1,0),
=(1,1,0), ![]() =(0,0,a),
=(0,0,a), ![]() =
= ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
),
取 ![]() =(1,﹣1,0),则
=(1,﹣1,0),则 ![]() 为面PAC的法向量.
为面PAC的法向量.
设 ![]() =(x,y,z)为面EAC的法向量,则
=(x,y,z)为面EAC的法向量,则 ![]()
取x=a,y=﹣a,z=﹣2,则 ![]() =(a,﹣a,﹣2),
=(a,﹣a,﹣2),
依题意,|cos< ![]() ,
, ![]() >|=
>|= ![]() =
= ![]() ,则a=1.
,则a=1.
于是 ![]() =(1,﹣1,﹣2),
=(1,﹣1,﹣2), ![]() =(1,1,﹣2).
=(1,1,﹣2).
设直线PA与平面EAC所成角为θ,则sinθ=|cos< ![]() >|=
>|= ![]() =
= ![]() ,
,
即直线PA与平面EAC所成角的正弦值为 ![]() .
.
【解析】(1)取线段AB的中点F,连接EF,CF,证明四边形ADCF是平行四边形,进而证明面CFE∥面PAD,即可证明EC∥平面PAD;(2)根据题意,建立空间直角坐标系,用坐标表示点与向量,求出面PAC的法向量,面EAC的法向量,利用二面角P﹣A C﹣E的余弦值为 ![]() ,可求a的值,从而可求
,可求a的值,从而可求 ![]() ,利用向量的夹角公式即可求得直线PA与平面EAC所成角的正弦值.
,利用向量的夹角公式即可求得直线PA与平面EAC所成角的正弦值.
【考点精析】利用直线与平面平行的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有 ![]() >0.
>0.
(Ⅰ)证明f(x)在[﹣1,1]上是增函数;
(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0
(Ⅲ)若f(x)≤t2﹣2at+1对x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x∈R)
(x∈R)
(1)用定义证明f(x)是增函数;
(2)若g(x)=f(x)﹣a是奇函数,求g(x)在(﹣∞,a]上的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣(m﹣1)x+2m
(1)若函数f(x)>0在(0,+∞)上恒成立,求m的取值范围;
(2)若函数f(x)在(0,1)内有零点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 单调递增,其中
单调递增,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,当
,当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小关系(其中
的大小关系(其中![]() 是
是![]() 的导函数),请写出详细的推理过程;
的导函数),请写出详细的推理过程;
(3)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
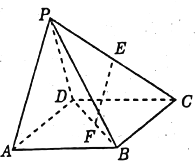
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等腰三角形,
为等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com