
【题目】已知函数f(x)=x﹣ ![]() .
.
(1)利用定义证明:函数f(x)在区间(0,+∞)上为增函数;
(2)当x∈(0,1)时,tf(2x)≥2x﹣1恒成立,求实数t的取值范围.
【答案】
(1)证明:任取x1、x2∈(0,+∞),且x1<x2,
则f(x1)﹣f(x2)=(x1﹣ ![]() )﹣(x2﹣
)﹣(x2﹣ ![]() )=
)= ![]() ,
,
∵0<x1<x2,∴1+x1x2>0,x1x2>0,x1﹣x2<0,
∴ ![]() <0,
<0,
即f(x1)﹣f(x2)<0,
∴f(x1)<f(x2),
∴函数f(x)在区间(0,+∞)上为增函数
(2)解:∵t(2x﹣ ![]() )≥2x﹣1,
)≥2x﹣1,
∴ ![]() ≥2x﹣1
≥2x﹣1
∵x∈(0,1],∴1<2x≤2,
∴t≥ ![]() 恒成立,设g(x)=
恒成立,设g(x)= ![]() =1﹣
=1﹣ ![]() ,
,
显然g(x)在 (0,1]上为增函数,
g(x)的最大值为g(1)= ![]() ,故t的取值范围是[
,故t的取值范围是[ ![]() ,+∞)
,+∞)
【解析】1、由定义法证明函数的单调性。
2、根据指数函数的单调性可得当x∈(0,1],∴1<2x≤2 ,![]() 恒成立,设
恒成立,设![]() g(x)在 (0,1]上为增函数,g(x)的最大值为g(1)=
g(x)在 (0,1]上为增函数,g(x)的最大值为g(1)= ![]() .t的取值范围是[
.t的取值范围是[ ![]() ,+∞)
,+∞)
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某农场种植黄瓜,根据多年的市场行情得知,从春节起的300天内,黄瓜市场售价与上市时间的关系用图1所示的一条折线表示,黄瓜的种植成本与上市时间的关系用图2所示的抛物线表示.(注:市场售价和种植成本的单位:元/kg,时间单位:天)
(1)写出图1表示的市场售价与时间的函数关系式P=f(t);写出图2表示的种植成本与时间的函数关系式Q=g(x);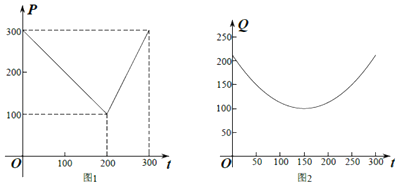
(2)认定市场售价减去种植成本为纯收益,问从春节开始的第几天上市的黄瓜纯收益最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各小题中,p是q的充分不必要条件的是( ) ①p:m<﹣2或m>6,q:y=x2+mx+m+3有两个零点;
② ![]() ,q:y=f(x)是偶函数;
,q:y=f(x)是偶函数;
③p:cosα=cosβ,q:tanα=tanβ;
④p:A∩B=A,q:(UB)(UA)
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+a2﹣1.
(1)若对任意的x∈R均有f(1﹣x)=f(1+x),求实数a的值;
(2)当x∈[﹣1,1]时,求f(x)的最小值,用g(a)表示其最小值,判断g(a)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线y 2=﹣8x的焦点,O为原点,点P是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO|的最小值为( )
A.6
B.![]()
C.![]()
D.4+2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程是 ![]() (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2+12ρcosθ+11=0. (Ⅰ)说明C是哪种曲线?并将C的方程化为直角坐标方程;
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2+12ρcosθ+11=0. (Ⅰ)说明C是哪种曲线?并将C的方程化为直角坐标方程;
(Ⅱ)直线l与C交于A,B两点,|AB|= ![]() ,求l的斜率.
,求l的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com