
【题目】已知数列{an}的前n项和为Sn , a1=1,an+1= ![]() Sn . 求证:
Sn . 求证:
(1)数列{ ![]() }成等比;
}成等比;
(2)Sn+1=4an .
【答案】
(1)证明:∵数列{an}的前n项和为Sn,a1=1,an+1= ![]() Sn,
Sn,
∴Sn= ![]() ,Sn﹣1=
,Sn﹣1= ![]() ,n≥2
,n≥2
∴an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() ,
,
即2n× ![]() =
= ![]() ,
,
∵n≠0,∴ ![]() =
= ![]() ,
,
∴ ![]() ,(n≥2)
,(n≥2)
即 ![]() :
: ![]() =2,
=2,
n=1时, ![]() =
= ![]() =1,
=1,
∴{ ![]() }是首项为1,公比为2的等比数列.
}是首项为1,公比为2的等比数列.
(2)证明:∵{ ![]() }是首项为1,公比为2的等比数列,
}是首项为1,公比为2的等比数列,
∴ ![]() =2n﹣1,∴Sn=n2n﹣1,
=2n﹣1,∴Sn=n2n﹣1,
∴an+1= ![]() Sn=
Sn= ![]() =(n+2)2n﹣1,
=(n+2)2n﹣1,
∴an=(n+1)2n﹣2.
∴Sn+1=(n+1)2n=4an.
【解析】(1)由an+1= ![]() Sn , 知Sn﹣Sn﹣1=
Sn , 知Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() ,从而
,从而 ![]() =
= ![]() ,进而
,进而 ![]() ,(n≥2),由此能证明{
,(n≥2),由此能证明{ ![]() }是首项为1,公比为2的等比数列.(2)由(1)可知Sn=n2n﹣1 , an=(n+1)2n﹣2 . 由此能证明Sn+1=(n+1)2n=4an .
}是首项为1,公比为2的等比数列.(2)由(1)可知Sn=n2n﹣1 , an=(n+1)2n﹣2 . 由此能证明Sn+1=(n+1)2n=4an .
【考点精析】利用等比关系的确定和数列的通项公式对题目进行判断即可得到答案,需要熟知等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2-10x3(单位:万元),成本函数为C(x)=460x-5 000(单位:万元).
(1)求利润函数P(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 平面
平面![]() .
.
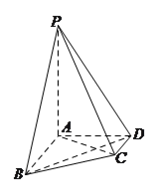
(1)设平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求证: ![]() .
.
(3)设点![]() 为线段
为线段![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足:Sn=n2 , 等比数列{bn}满足:b2=2,b5=16
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)若圆![]() 的切线在
的切线在![]() 轴和
轴和![]() 轴上的截距相等,求此切线的方程.
轴上的截距相等,求此切线的方程.
(2)从圆![]() 外一点
外一点![]() 向该圆引一条切线,切点为
向该圆引一条切线,切点为![]() ,
, ![]() 为坐标原点,且有
为坐标原点,且有![]() ,求使得
,求使得![]() 取得最小值的点
取得最小值的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内的动点P到定直线l:x=![]() 的距离与点P到定点F(
的距离与点P到定点F(![]() ,0)之比为
,0)之比为![]() .
.
(1)求动点P的轨迹C的方程;
(2)若点N为轨迹C上任意一点(不在x轴上),过原点O作直线AB,交(1)中轨迹C于点A、B,且直线AN、BN的斜率都存在,分别为k1、k2,问k1·k2是否为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
(2017天津)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟) | 广告播放时长(分钟) | 收视人次(万) | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用![]() ,
,![]() 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.
(1)用![]() ,
,![]() 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com