
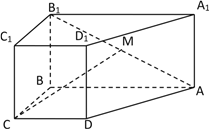
【题目】如图,四棱柱ABCD-A1B1C1D1中,CD∥AB, AB⊥BC,AB=BC=2CD=2,侧棱AA1⊥平面ABCD.且点M是AB1的中点
(1)证明:CM∥平面ADD1A1;
(2)求点M到平面ADD1A1的距离.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)根据题意得到四边形AECD为平行四边形,∴CE∥AD,∴CE∥平面![]() ,进而得到面面平行,再得到线面平行;(2)根据等体积法得到
,进而得到面面平行,再得到线面平行;(2)根据等体积法得到![]() ,列式求得
,列式求得![]() .
.
解析:
(1)取AB的中点E,连结CE、ME.
∵M为AB1的中点 ∴ME∥BB1∥AA1
又∵AA1![]() 平面ADD1A1 ∴ME∥平面ADD1A1
平面ADD1A1 ∴ME∥平面ADD1A1
又∵AB∥CD,CD= ![]() AB ∴AE平行且等于CD ∴四边形AECD为平行四边形 ∴CE∥AD又∵AD
AB ∴AE平行且等于CD ∴四边形AECD为平行四边形 ∴CE∥AD又∵AD![]() 平面ADD1A1 ∴CE∥平面ADD1A1
平面ADD1A1 ∴CE∥平面ADD1A1
又∵ME∩CE=E ∴平面CME∥平面ADD1A1
又∵CM![]() 平面CME ∴CM∥平面ADD1A1
平面CME ∴CM∥平面ADD1A1
(2)由(1)可知CM∥平面ADD1A1,所以M到平面ADD1A1的距离等价于C到平面ADD1A1的距离,不妨设为h,则![]() .
.
![]()
在梯形ABCD中,可计算得AD= ![]() ,
,
则![]()
∴![]() =
= ![]() ,得
,得![]() ,即点M到平面ADD1A1的距离
,即点M到平面ADD1A1的距离![]()


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为![]() ,
,![]() ,…,
,…,![]() ).
).

(1)求成绩在![]() 的频率,并补全此频率分布直方图;
的频率,并补全此频率分布直方图;
(2)求这次考试平均分的估计值;
(3)若从成绩在![]() 和
和![]() 的学生中任选两人,求他们的成绩在同一分组区间的概率.
的学生中任选两人,求他们的成绩在同一分组区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域是R上的奇函数![]() .
.
(1)求a;
(2)判断![]() 在R上的单调性,并用定义法证明;
在R上的单调性,并用定义法证明;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(4)设关于x方程![]() 有零点,求实数b的取值范围.
有零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() ,
,![]() 两组.
两组.![]() 年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() ,
,![]() ,
,![]() ,
,![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组:![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:
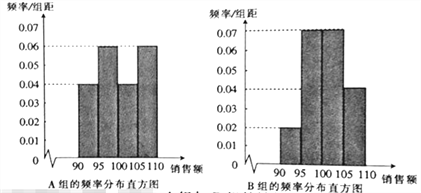
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() ,
,![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)在如图所示给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间;
(3)由图象指出当x取什么值时f(x)有最值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区的区人大代表有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为![]() ,乙校教师记为
,乙校教师记为![]() ,丙校教师记为
,丙校教师记为![]() ,丁校教师记为
,丁校教师记为![]() .现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
.现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
(1)请列出十九大报告宣讲团组成人员的全部可能结果;
(2)求教师![]() 被选中的概率;
被选中的概率;
(3)求宣讲团中没有乙校教师代表的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左、右焦点为F1、F2,点P是坐标平面内一点,且
,其左、右焦点为F1、F2,点P是坐标平面内一点,且![]() 其中O为坐标原点。
其中O为坐标原点。
(I) 求椭圆C的方程;
(II) 如图,过点S(0,![]() },且斜率为k的动直线l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
},且斜率为k的动直线l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com