
【题目】已知p:关于x的不等式x2+2ax+4>0对一切 ![]() 恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
A.![]()
B.B、
C.C、
D.a≥-2
 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+a+1.
(1)当a=1时,求函数在区间[﹣2,3]上的值域;
(2)函数f(x)在[﹣5,5]上单调,求实数a的取值范围;
(3)求函数f(x)在[0,2]上的最小值g(a)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校拟建一块周长为400m的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽? 
查看答案和解析>>
科目:高中数学 来源: 题型:
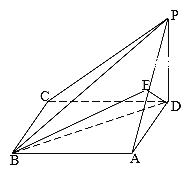
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E分别为AP的中点.
(Ⅰ)求证:DE垂直于平面PAB;
(Ⅱ)设BC =![]() ,AB=2,求直线EB与平面ABD所成的角的大小.
,AB=2,求直线EB与平面ABD所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() (a∈R)g(x)=lnx.
(a∈R)g(x)=lnx.
(1)若对任意的实数a,函数f(x)与g(x)的图象在x=x0处的切线斜率总相等,求x0的值;
(2)若a>0,对任意x>0,不等式f(x)﹣g(x)≥1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)定义域中任意的x1 , x2(x1≠x2)有如下结论
1)f(x1+x2)=f(x1)f(x2)
2)f(x1x2)=f(x1)+f(x2)
3) ![]() >0
>0
4)f( ![]() )<
)< ![]()
5)f( ![]() )>
)> ![]()
6)f(﹣x)=f(x).
当f(x)=lgx时,上述结论正确的序号为 . (注:把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的不等式x2+2ax+4>0对一切 ![]() 恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
A.![]()
B.B、
C.C、
D.a≥-2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式x2﹣(a2+3a+2)x+3a(a2+2)<0(a∈R).
(Ⅰ)解该不等式;
(Ⅱ)定义区间(m,n)的长度为d=n﹣m,若a∈R,求该不等式解集表示的区间长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①原命题为真,它的否命题为假;
②原命题为真,它的 逆命题不一定为真;
③若命题的逆命题为真,则它的否命题一定为真;
④若命题的逆否命题为真,则它的否命题一定为真;
⑤“若 m>1 ,则 mx2-2(m+1)x+m+3>0 的解集为R”的逆命题.
其中真命题是.(把你认为正确命题的序号都填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com