
分析 (Ⅰ)通过设数列{an}的公差为d,数列{bn}的公比为q,分别在a1b1+a2b2+a3b3+…+anbn=(n-1)•2n+2+4中令n=1,2,3,进而计算即得结论;
(Ⅱ)通过an=2n可知cos$\frac{{a}_{n+1}}{2}$π=(-1)n+1,设bn=$\frac{1}{(1-\frac{1}{{a}_{1}})(1-\frac{1}{{a}_{2}})…(1-\frac{1}{{a}_{n}})\sqrt{{a}_{n}+1}}$,进而不等式等价于(-1)n+1λ<bn,分n为奇数、偶数两种情况讨论即可;
(Ⅲ)当d=0显然满足题意,当d>0时,利用a1007=2014可知c1=2014-38d,进而可知ck=2014+(k-39)d,化简${{c}_{39}}^{2}$=c1ck可知k=39+$\frac{53×38}{53-d}$∈N*,结合c1、d>0计算即得结论.
解答 解:(Ⅰ)设数列{an}的公差为d,数列{bn}的公比为q,
∵a1b1+a2b2+a3b3+…+anbn=(n-1)•2n+2+4对任意的n∈N*恒成立,
∴当n=1,2,3时,分别可得a1b1=4,a1b1+a2b2=20,a1b1+a2b2+a3b3=68,
又∵a1=2,
∴b1=$\frac{4}{{a}_{1}}$=2,且$\left\{\begin{array}{l}{{a}_{2}{b}_{2}=16}\\{{a}_{3}{b}_{3}=48}\end{array}\right.$,
即$\left\{\begin{array}{l}{(2+d)(2q)=16}\\{(2+2d)(2{q}^{2})=48}\end{array}\right.$,消去q整理得:3d2-4d-4=0,
解得:d=2或-$\frac{2}{3}$(舍),
∴q=2,an=2n,bn=2n;
(Ⅱ)结论:存在非零整数λ=±1满足条件.
理由如下:
由an=2n,得cos$\frac{{a}_{n+1}}{2}$π=cos(n+1)π=(-1)n+1,
设bn=$\frac{1}{(1-\frac{1}{{a}_{1}})(1-\frac{1}{{a}_{2}})…(1-\frac{1}{{a}_{n}})\sqrt{{a}_{n}+1}}$,则不等式等价于(-1)n+1λ<bn,
∵bn>0,且$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{2(n+1)}{\sqrt{2n+1}•\sqrt{2n+3}}$>1,
∴bn+1>bn,数列{bn}单调递增.
假设存在这样的实数λ,使得不等式(-1)n+1λ<bn对一切n∈N*都成立,则:
①当n为奇数时,得λ<(bn)min=b1=$\frac{2\sqrt{3}}{3}$;
②当n为偶数时,得-λ<(bn)min=b2=$\frac{8\sqrt{5}}{15}$,即λ>-$\frac{8\sqrt{5}}{15}$;
综上,λ∈(-$\frac{8\sqrt{5}}{15}$,$\frac{2\sqrt{3}}{3}$),由λ是非零整数可知λ=±1满足条件;
(Ⅲ)易知d=0,成立;
当d>0时,c39=c1+38d=2014,c1=2014-38d,
ck=c39+(k-39)d=2014+(k-39)d,
∵${{c}_{39}}^{2}$=c1ck,
∴(2014-38d)[2014+(k-39)d]=20142,
∴38(53-d)[2014+(k-39)d]=20142,
∴(53-d)[2014+(k-39)d]=53×2014,
∴-(k-39)d2+53(k-77)d=0,
∴(k-39)d=53(k-77),
∴(d-53)k=39d-53×77,
∴k=$\frac{39d-53×77}{d-53}$=$\frac{39(d-53)+53×39-53×77}{d-53}$=39-$\frac{53×38}{d-53}$=39+$\frac{53×38}{53-d}$∈N*,
又∵c1=2014-38d=38(53-d)>0,d>0,
∴0<53-d<53,
∴53-d=1,2,19,38,
∴d=52,51,34,15,
于是公差d的所有可能取值之和为152.
点评 本题考查数列的通项,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于难题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
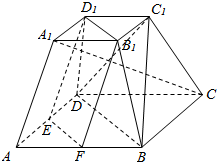 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1或-1 | C. | $\frac{1}{2}$或$-\frac{1}{2}$ | D. | 2或-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com