
【题目】设函数f(x)=lnx﹣ax(a∈R).
(1)若直线y=3x﹣1是函数f(x)图象的一条切线,求实数a的值;
(2)若函数f(x)在[1,e2]上的最大值为1﹣ae(e为自然对数的底数),求实数a的值;
(3)若关于x的方程ln(2x2﹣x﹣3t)+x2﹣x﹣t=ln(x﹣t)有且仅有唯一的实数根,求实数t的取值范围.
【答案】
(1)解:由f(x)=lnx﹣ax,得f′(x)= ![]() =3,
=3,
∴x= ![]() ,则f(
,则f( ![]() )=ln
)=ln ![]() ﹣
﹣ ![]() ,
,
∴ln ![]() ﹣
﹣ ![]() =
= ![]() -1,得ln
-1,得ln ![]() =0,即a=﹣2
=0,即a=﹣2
(2)解:f′(x)= ![]() ,
,
当a≤ ![]() 时,f′(x)≥0在[1,e2]上恒成立,故f(x)在[1,e2]上为增函数,
时,f′(x)≥0在[1,e2]上恒成立,故f(x)在[1,e2]上为增函数,
故f(x)的最大值为f(e2)=2﹣ae2=1﹣ae,得 ![]() (舍);
(舍);
当 ![]() <a<1时,若x∈[1,
<a<1时,若x∈[1, ![]() ],f′(x)>0,x∈[
],f′(x)>0,x∈[ ![]() ,2],f′(x)<0,
,2],f′(x)<0,
故f(x)在[1,e2]上先增后减,故 ![]() ,
,
f(1)=﹣a,f(e2)=2﹣ae2,
即当 ![]() 时,
时, ![]() ,得
,得 ![]() (舍);
(舍);
当 ![]() 时,f(x)max=﹣a=1﹣ae,得a=
时,f(x)max=﹣a=1﹣ae,得a= ![]() ;
;
当a≥1时,故当x∈[1,e2]时,f′(x)≤0,f(x)是[1,e2]上的减函数,
故f(x)max=f(1)=﹣a=1﹣ae,得a= ![]() (舍);
(舍);
综上,a= ![]()
(3)ln(2x2﹣x﹣3t)+x2﹣x﹣t=ln(x﹣t)ln(2x2﹣x﹣3t) ![]() (2x2﹣x﹣3t)=ln(x﹣t)
(2x2﹣x﹣3t)=ln(x﹣t) ![]() (x﹣t),
(x﹣t),
令g(x)=lnx+ ![]() ,则g(x)在(0,+∞)上是增函数,
,则g(x)在(0,+∞)上是增函数,
又g(2x2﹣x﹣3t)=g(x﹣t),
∴2x2﹣x﹣3t=x﹣t2(x2﹣x﹣t)=0,
即 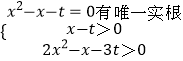
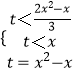 ,
,
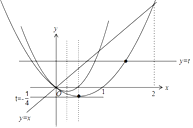
作出图象如图:由图可知,实数t的取值范围是t=﹣ ![]() 或0<t<2.
或0<t<2.
【解析】(1)求出原函数的导函数,得到x= ![]() ,求出f(
,求出f( ![]() )=ln
)=ln ![]() ﹣
﹣ ![]() ,代入直线y=3x﹣1求得a值;(2)求出原函数的导函数,然后对a分类得到函数在[1,e2]上的单调性,并进一步求出函数在[1,e2]上的最大值,由最大值等于1﹣ae求得a值;(3)把ln(2x2﹣x﹣3t)+x2﹣x﹣t=ln(x﹣t)转化为ln(2x2﹣x﹣3t)
,代入直线y=3x﹣1求得a值;(2)求出原函数的导函数,然后对a分类得到函数在[1,e2]上的单调性,并进一步求出函数在[1,e2]上的最大值,由最大值等于1﹣ae求得a值;(3)把ln(2x2﹣x﹣3t)+x2﹣x﹣t=ln(x﹣t)转化为ln(2x2﹣x﹣3t) ![]() (2x2﹣x﹣3t)=ln(x﹣t)
(2x2﹣x﹣3t)=ln(x﹣t) ![]() (x﹣t),构造函数g(x)=lnx+
(x﹣t),构造函数g(x)=lnx+ ![]() ,则g(x)在(0,+∞)上是增函数,得到
,则g(x)在(0,+∞)上是增函数,得到 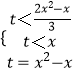 ,画出图形,数形结合得答案.
,画出图形,数形结合得答案.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中 ![]() 是这7个数据的平均数),则输出的S的值是( )
是这7个数据的平均数),则输出的S的值是( )
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |

A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).则分数在[70,80)内的人数是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(2,0),B(0,2),C(cosα,sinα).
(1)若 ![]() ,且α∈(0,π),求角α的值;
,且α∈(0,π),求角α的值;
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2lnx﹣ ![]() ﹣m,若关于x的方程f(f(x))=x恰有两个不相等的实数根,则m的取值范围是( )
﹣m,若关于x的方程f(f(x))=x恰有两个不相等的实数根,则m的取值范围是( )
A.(2ln3﹣4,+∞)
B.(﹣∞,2ln3﹣4)
C.(﹣4,+∞)
D.(﹣∞,﹣4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2.5cos(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( )
)的部分图象如图所示,M、N两点之间的距离为13,且f(3)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数的图象关于坐标原点对称,则t的最小值为( ) 
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
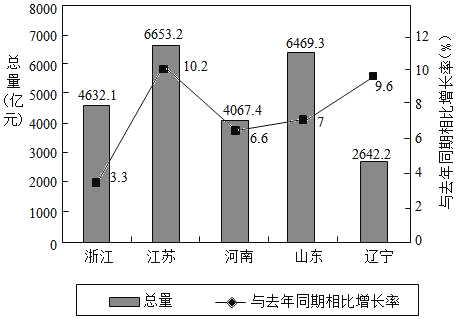
A. 2017年第一季度![]() 总量和增速由高到低排位均居同一位的省只有1个
总量和增速由高到低排位均居同一位的省只有1个
B. 与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长
总量均实现了增长
C. 去年同期河南省的![]() 总量不超过4000亿元
总量不超过4000亿元
D. 2017年第一季度![]() 增速由高到低排位第5的是浙江省
增速由高到低排位第5的是浙江省
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com