
【题目】已知首项为 ![]() 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.
【答案】
(1)解:设等比数列的公比为q,
∵S3+a3,S5+a5,S4+a4成等差数列.
∴S5+a5﹣(S3+a3)=S4+a4﹣(S5+a5)
即4a5=a3,
故q2= ![]() =
= ![]()
又∵数列{an}不是递减数列,且等比数列的首项为 ![]()
∴q=﹣ ![]()
∴数列{an}的通项公式an= ![]() ×(﹣
×(﹣ ![]() )n﹣1=(﹣1)n﹣1
)n﹣1=(﹣1)n﹣1 ![]()
(2)解:由(1)得
Sn=1﹣(﹣ ![]() )n=
)n= 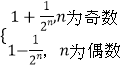
当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1= ![]()
故0< ![]() ≤
≤ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]()
当n为偶数时,Sn随n的增大而增大,所以1>Sn≥S2= ![]()
故0> ![]() ≥
≥ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]()
综上,对于n∈N*,总有 ![]() ≤
≤ ![]() ≤
≤
故数列{Tn}的最大项的值为 ![]() ,最小项的值为
,最小项的值为 ![]()
【解析】(1)设等比数列的公比为q,由S3+a3 , S5+a5 , S4+a4成等差数列,可构造关于q的方程,结合首项为 ![]() 的等比数列{an}不是递减数列,求出q值,可得答案.(2)由(1)可得Sn的表达式,由于数列为摆动数列,故可分类讨论求出
的等比数列{an}不是递减数列,求出q值,可得答案.(2)由(1)可得Sn的表达式,由于数列为摆动数列,故可分类讨论求出 ![]() 在n为奇数和偶数时的范围,综合讨论结果,可得答案.
在n为奇数和偶数时的范围,综合讨论结果,可得答案.
【考点精析】根据题目的已知条件,利用等比数列的通项公式(及其变式)和数列的前n项和的相关知识可以得到问题的答案,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系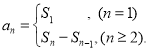 .
.


科目:高中数学 来源: 题型:
【题目】设f(x)=a(x﹣5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的16%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金y(单位:万元),销售利润x(单位:万元)
(1)写出该公司激励销售人员的奖励方案的函数模型;
(2)如果业务员老张获得5.6万元的奖金,那么他的销售利润是多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,共可得到lga﹣lgb的不同值的个数是( )
A.9
B.10
C.18
D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法, 某化学老师分别用传统教学和“新课堂”两种不同的教学方式, 在甲、乙两个平行班进行教学实验, 为了解教学效果, 期中考试后, 分别从两个班级中各随机抽取20名学生的成绩进行统计, 作出的茎叶图如下图, 记成绩不低于70分者为“成绩优良”.
(1) 分别计算甲、乙两班20个样本中, 化学成绩前十的平均分, 并据此判断哪种教学方式的教学效果更佳;
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总 计 |
(2)由以上统计数据填写下面2×2列联表,是否有95%的把握认为“成绩优良与教学方式关”?
| 0.05 | 0.010 |
| 3.841 | 6.635 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002,…,800进行编号.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42.
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
| 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
①若在该样本中,数学成绩优秀率是30%,求a,b的值:
②在地理成绩及格的学生中,已知![]() 求数学成绩优秀的人数比及格的人数少的概率.
求数学成绩优秀的人数比及格的人数少的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com