
����Ŀ��Ϊ�˲μ��и������������ij��ѧ�������ĸ������ǿ�İ༶�������Ա��ѡ��![]() �������������ӣ������õ����������ĸ������ǿ�İ༶�����Ա�������±���
�������������ӣ������õ����������ĸ������ǿ�İ༶�����Ա�������±���
�༶ | ������7���� | ������17���� | �߶���31���� | �߶���32���� |
���� | 12 | 6 | 9 | 9 |
��1���ֲ�ȡ�ֲ�����ķ��������ĸ����г�ȡ�˶�Ա����Ӧ�ֱ�����ĸ������Ķ�Ա������
��2������ѧ����ӷ���ƴ������ùھ�.��Ҫ�Ӹ����꼶����Ķ�Ա��ѡ����λ��Ա��Ϊ�ھ��Ĵ������ԣ���ѡ����������Ա����ͬһ��ĸ���.
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() ����2��
����2��![]() .
.
��������
�����������1���������֪�������ÿ�����屻�鵽�ĸ��ʣ����ø�����������Ա�������Դ˸��ʣ����÷ֱ�����ĸ������Ķ�Ա��������2�������оٷ������п�������оٳ�����������Ҫ��ĸ���..
�����������1������֪��Ӧ�Ӹ�����![]() �����г��
�����г��![]() �ˣ�
�ˣ�
Ӧ�Ӹ�����![]() �����г��
�����г��![]() �ˣ�Ӧ�Ӹ߶���
�ˣ�Ӧ�Ӹ߶���![]() �����г��
�����г��![]() �ˣ�
�ˣ�
Ӧ�Ӹ߶���![]() �����г��
������![]() ��.
��.
��2���Ǹ�����![]() ��������
��������![]() ��Ϊ
��Ϊ![]() ��������
��������![]() ������������Ϊ
������������Ϊ![]() ��
��
�����![]() ����
���г��![]() �˵Ļ����¼��У�
�˵Ļ����¼��У�![]()
![]()
![]()
![]() ��
��![]() ����
����
���������![]() ������ͬһ����Ϊ�¼�
������ͬһ����Ϊ�¼�![]() �����¼�
�����¼�![]() ����
����![]()
![]()
![]()
![]() ��
��![]() ������
������![]() .
.


 �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��4������ϵ���������
��ƽ��ֱ������ϵ�У���ֱ֪��![]() ����
����![]() �����
����б��![]() ������ԭ��Ϊ���㣬
������ԭ��Ϊ���㣬![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��
������д��ֱ��![]() �IJ������̺�����
�IJ������̺�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��������ֱ��![]() ������
������![]() �ֱ���
�ֱ���![]() ��
��![]() ���㣬��
���㣬��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������![]() �У�����
�У�����![]() ��ֱ�������Σ�
��ֱ�������Σ�![]() ��
��![]() ����
Ϊ����![]() ���е�.
���е�.
��1��������ֱ��![]() ��
��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��2��������![]() ��ƽ��ǵ�����ֵ.
��ƽ��ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �÷�֤��֤�����⣺�������������ڽ�������һ��������60�㡱ʱ��Ӧ������ ��
A�������ڽǶ�������60�� B�������ڽǶ�����60��
C�������ڽ�������һ������60�� D�������ڽ���������������60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
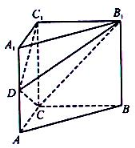
����Ŀ����֪������P��ABCD��ͼ��
��������������ͼ��һ���߳��ֱ�Ϊ![]() ��
��![]() ��2�ĵ��������Σ���������S�����V��
��2�ĵ��������Σ���������S�����V��
��������AB�е�ΪM��PC�е�ΪN��֤����MN��ƽ��PAD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
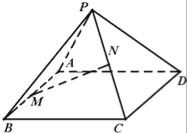
����Ŀ����ͼ��������![]() �У�
��![]() ����
����![]() ������
������![]() �Ǿ��Σ�
�Ǿ��Σ�![]() ��
��![]() ��
��![]() ���е�.
���е�.
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����֪��![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() ��һ�㣬��ƽ��
��һ�㣬��ƽ��![]() ƽ��
ƽ��![]() .��
.��![]() �����
�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
������![]() ��
��![]() ��ȡ�ü�ֵ����
��ȡ�ü�ֵ����![]() ��ֵ��
��ֵ��
������![]() ������
������![]() �ϵ�������, ��
�ϵ�������, ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�������ۺ���![]() ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
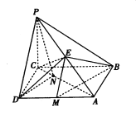
����Ŀ����ͼ��ʾ��������![]() �У�����
������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е�.
���е�.

��1��֤����![]() ��
��
��2��������![]() ������ֵ��
������ֵ��
��3�����![]() ���߶�
���߶�![]() �ϣ���ֱ��
�ϣ���ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() �����߶�
�����߶�![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ������һ�ֵ��Ӳ�Ʒ�ijɱ���ÿ��500Ԫ���ƻ��ڽ���3���ڣ�ʹ�ɱ����͵�ÿ��256Ԫ����ƽ��ÿ��ɱ�Ӧ����(����)
A. 10% B. 15% C. 20% D. 25%
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com