练习册

  • 练习册
  • 试题
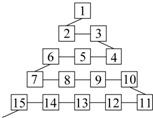    精英家教网 > 高中数学 > 题目详情
    如图是从事网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4（从左至右）出现在第3行；数字7，8，9，10出现在第4行；依此类推．则第27行从左至右算第8个数字是
    371
    371
    ．
    分析：注意数字排列的规律，每行的行号数和这一行的数字的个数相同，奇数行的数字从左向右依次减小，偶数行的数字从左向右依次增大，每行中相邻的数字为连续正整数，求出第27行最左边的一个数即可求出所求．
    解答：解：由每行的行号数和这一行的数字的个数相同，奇数行的数字从左向右依次减小，偶数行的数字从左向右依次增大，
    第27行的数字从左向右依次减小，可求出第27行最左边的一个数是
    27(27+1)
    2
    =378，
    从左至右的第8个数应是378-7=371．
    故答案为：371
    点评：本题主要考查了等差数列求前n项和的公式，要善于观察，学会归纳总结，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图是从事网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4（从左至右）出现在第3行；数字7，8，9，10出现在第4行；依此类推．则第99行从左至右算第3个数字是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图是从事网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4（从左至右）出现在第3行；数字7，8，9，10出现在第4行；依此类推．若2013是第m行从左至右算的第n个数字，则（m，n）为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•宝坻区一模）如图是从事网络工作者经常用来解释网络运作的蛇形模型，数字1出现在第1行；数字2、3出现在第2行；数字6、5、4（从左至右）出现在第3行；数字7、8、9、10出在第4行；依此类推．试问第50行，从左至右算，第7个数字为
    1232；
    1232；
    ．

    查看答案和解析>>

    科目：高中数学 来源：2014届浙江省高二上学期期末考试理科数学试卷（解析版） 题型：选择题

    如图是从事网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4（从左至右）出现在第3行；数字7，8，9，10出现在第4行；依此类推．若2013是第m行从左至右算的第n个数字，则（m，n）为（  ）

    A．（63，60）        B．（63，4）         C．（64，61）        D．（64，4）

     

    查看答案和解析>>

    同步练习册答案