
【题目】已知数列{an}满足a1=1,a2=4,且对任意m,n,p,q∈N* , 若m+n=p+q,则有am+an=ap+aq . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{ ![]() }的前n项和为Sn , 求证:
}的前n项和为Sn , 求证: ![]() ≤Sn<
≤Sn< ![]() .
.
【答案】(Ⅰ)解:令m=1,p=n﹣1,q=2,可得:an+a1=an﹣1+a2 , 即an﹣an﹣1=3.(n≥2). ∴数列{an}是等差数列,公差为3.
∴an=1+3(n﹣1)=3n﹣2.
(Ⅱ)证明: ![]() =
= ![]() =
= ![]() .
.
∴Sn= ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() <
< ![]() .
.
另一方面:数列 ![]() 单调递增,∴Sn≥S1=
单调递增,∴Sn≥S1= ![]() .
.
∴ ![]() ≤Sn<
≤Sn< ![]()
【解析】(I)令m=1,p=n﹣1,q=2,可得:an+a1=an﹣1+a2 , 即an﹣an﹣1=3.(n≥2).利用等差数列的通项公式即可得出.(II) ![]() =
= ![]() =
= ![]() .利用裂项求和方法与数列的单调性即可证明.
.利用裂项求和方法与数列的单调性即可证明.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
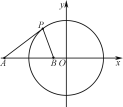
(1)求与圆C相切,且与直线l垂直的直线方程;
(2)在直线OA上(O为坐标原点),存在定点B(不同于点A),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点B的坐标.
为一常数,试求所有满足条件的点B的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知点A(-1,-2),B(1,3),P为x轴上的一点,求|PA|+|PB|的最小值;
(2)已知点A(2,2),B(3,4),P为x轴上一点,求||PB|-|PA||的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在路边安装路灯,灯柱![]() 的高为
的高为![]() 米,路宽
米,路宽![]() 为23米,灯杆
为23米,灯杆![]() 与灯柱
与灯柱![]() 角,路灯采用锥形灯罩,灯罩轴线
角,路灯采用锥形灯罩,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直,请你建立适当直角坐标系,解决以下问题:
垂直,请你建立适当直角坐标系,解决以下问题:
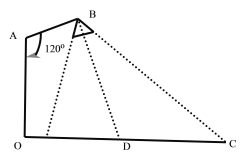
(1)当![]()
(2)![]() 且灯罩轴线
且灯罩轴线![]() 正好通过道路路面的中线时,求灯杆
正好通过道路路面的中线时,求灯杆![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3ax2﹣9a2x+a3 . 若a> ![]() ,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,则a的取值范围为( )
,且当x∈[1,4a]时,|f′(x)|≤12a恒成立,则a的取值范围为( )
A.( ![]() ,
, ![]() ]
]
B.( ![]() ,1]
,1]
C.[﹣ ![]() ,1]
,1]
D.[0, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:y2=2px(p>0)的焦点为F,抛物线上存在一点G到焦点的距离为3,且点G在圆C:x2+y2=9上. (Ⅰ)求抛物线C1的方程;
(Ⅱ)已知椭圆C2: ![]() =1(m>n>0)的一个焦点与抛物线C1的焦点重合,且离心率为
=1(m>n>0)的一个焦点与抛物线C1的焦点重合,且离心率为 ![]() .直线l:y=kx﹣4交椭圆C2于A、B两个不同的点,若原点O在以线段AB为直径的圆的外部,求k的取值范围.
.直线l:y=kx﹣4交椭圆C2于A、B两个不同的点,若原点O在以线段AB为直径的圆的外部,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 ![]() (θ为参数).以原点O为极点,x轴的非负半轴为极轴建立极坐标方程.
(θ为参数).以原点O为极点,x轴的非负半轴为极轴建立极坐标方程.
(1)求曲线C的极坐标方程;
(2)若直线l:θ=α(α∈[0,π),ρ∈R)与曲线C相交于A,B两点,设线段AB的中点为M,求|OM|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C上任意一点到![]() 的距离与到点
的距离与到点![]() 的距离之比均为
的距离之比均为![]() .
.
(1)求曲线C的方程;
(2)设点![]() ,过点
,过点![]() 作两条相异直线分别与曲线C相交于
作两条相异直线分别与曲线C相交于![]() 两点,且直线
两点,且直线![]() 和直线
和直线![]() 的倾斜角互补,求线段
的倾斜角互补,求线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学根据2002﹣2014年期间学生的兴趣爱好,分别创建了“摄影”、“棋类”、“国学”三个社团,据资料统计新生通过考核远拔进入这三个社团成功与否相互独立,2015年某新生入学,假设他通过考核选拔进入该校的“摄影”、“棋类”、“国学”三个社团的概率依次为m, ![]() ,n,已知三个社团他都能进入的概率为
,n,已知三个社团他都能进入的概率为 ![]() ,至少进入一个社团的概率为
,至少进入一个社团的概率为 ![]() ,且m>n.
,且m>n.
(1)求m与n的值;
(2)该校根据三个社团活动安排情况,对进入“摄影”社的同学增加校本选修字分1分,对进入“棋类”社的同学增加校本选修学分2分,对进入“国学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课字分分数的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com