练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，已知曲线的参数方程为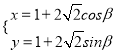（为参数），在极坐标系中，直线的方程为： ，直线的方程为．

    （Ⅰ）写出曲线的直角坐标方程，并指出它是何种曲线；

    （Ⅱ）设与曲线交于两点， 与曲线交于两点，求四边形面积的取值范围．

    【答案】(1) 以为圆心， 为半径的圆；（2）.

    【解析】试题分析：（Ⅰ）利用平方法可消去参数，从而可得曲线的直角坐标方程，进而得它是何种曲线；（Ⅱ）设， ，曲线的方程化成极坐标方程，将曲线的方程化成极坐标方程得： ，∴， ，从而可得结果.

    试题解析：（Ⅰ）由（为参数）消去参数得： ，

    ∴曲线是以为圆心， 为半径的圆．

    （Ⅱ）设， ，

    ∵三点共线，则①，

    将曲线的方程化成极坐标方程得： ，∴，代入①得： ，

    用代得：

    又∵，∴，

    ∴，

    ∵，∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】【2017湖南娄底二模】如图，四棱锥的底面是平行四边形，侧面是边长为2的正三角形， , .

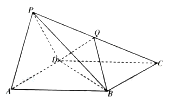
    （Ⅰ）求证：平面平面；

    （Ⅱ）设是棱上的点，当平面时，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（ ）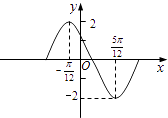

    A.y=2sin（2x+ ）
    B.y=2sin（2x+ ）
    C.y=2sin（ ﹣ ）
    D.y=2sin（2x﹣ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，AB//CD，且.

    （1）证明：平面PAB⊥平面PAD；

    （2）若PA=PD=AB=DC， ，求二面角A-PB-C的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，平面四边形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AD⊥ED，AF∥DE，AB∥CD，CD=2AB=2AD=2ED=xAF．
    （Ⅰ）若四点F、B、C、E共面，AB=a，求x的值；
    （Ⅱ）求证：平面CBE⊥平面EDB；
    （Ⅲ）当x=2时，求二面角F﹣EB﹣C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（ ，cos ）， =（cos ，1），且f（x）= ．
    （1）求函数f（x）的最小正周期；
    （2）求函数f（x）在区间[﹣π，π]上的最大值和最小值及取得最值时x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面向量 ， （ ≠ ）满足 =2，且 与 ﹣ 的夹角为120° ， t∈R，则|（1﹣t） +t |的最小值是 ． 已知 =0，向量 满足（ ﹣ ）（ ﹣ ）=0，| ﹣ |=5，| ﹣ |=3，则 的最大值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4―4：坐标系与参数方程]

    在直角坐标系xOy中，直线l1的参数方程为（t为参数），直线l2的参数方程为.设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．

    （1）写出C的普通方程；

    （2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ(cosθ+sinθ) =0，M为l3与C的交点，求M的极径.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用数学归纳法证明：12﹣22+32﹣42+…+（﹣1）n﹣1n2=（﹣1）n﹣1 ．

    查看答案和解析>>

    同步练习册答案