
【题目】已知椭圆![]() :
: ![]() 的长轴长为
的长轴长为![]() ,
, ![]() ,
, ![]() 是其长轴顶点,
是其长轴顶点, ![]() 是椭圆上异于
是椭圆上异于![]() ,
, ![]() 的动点,且
的动点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
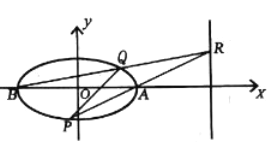
(2)如图,若动点![]() 在直线
在直线![]() 上,直线
上,直线![]() ,
, ![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
, ![]() 两点.请问:直线
两点.请问:直线![]() 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017安徽蚌埠一模)已知椭圆C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2
,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2![]() .
.

(1)求椭圆C的方程;
(2)设圆T:(x-2)2+y2=![]() ,过椭圆的上顶点M作圆T的两条切线交椭圆于E,F两点,求直线EF的斜率.
,过椭圆的上顶点M作圆T的两条切线交椭圆于E,F两点,求直线EF的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为:
的参数方程为: ![]() (
(![]() 为参数)
为参数)
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与圆
与圆![]() 相较于
相较于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )
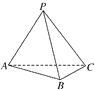
A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击手在同一条件下进行射击训练,结果如下:
射击次数n | 10 | 20 | 50 | 100 | 200 | 500 |
击中靶心次数m | 8 | 19 | 44 | 92 | 178 | 455 |
击中靶心频率 |
(1)求出表中击中靶心的各个频率值;
(2)这个射击手射击一次,击中靶心的概率可估计为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com