
【题目】已知数列{an}的前n项和Sn满足(p﹣1)Sn=p2﹣an(p>0,p≠1),且a3= ![]() .
.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bnbn+2}的前n项和为Tn , 若对于任意的正整数n,都有Tn<m2﹣m+
,数列{bnbn+2}的前n项和为Tn , 若对于任意的正整数n,都有Tn<m2﹣m+ ![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
【答案】
(1)解:依题意,(p﹣1)S1=p2﹣a1(p>0,p≠1),
∴a1=p,
∴(p﹣1)(p+a2)=p2﹣a2,解得:a2=1,
∴(p﹣1)(1+p+a3)=p2﹣a3,
又∵a3= ![]() ,
,
∴(p﹣1)(1+p+ ![]() )=p2﹣
)=p2﹣ ![]() ,解得:p=3,
,解得:p=3,
∴2Sn=9﹣an,
∴2an+1=an﹣an+1,即an+1= ![]() an,
an,
又∵a1=p=3,
∴数列{an}是首项为3,公比为 ![]() 的等比数列,
的等比数列,
∴an= ![]() =
= ![]() ;
;
(2)解:由(1)可知bn= ![]() =
= ![]() =
= ![]() ,
,
∴bnbn+2= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
∴Tn= ![]() (1﹣
(1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
= ![]() (1+
(1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )
)
= ![]() ﹣
﹣ ![]() (
( ![]() +
+ ![]() ),
),
显然Tn随着n的增大而增大,且Tn< ![]() ,
,
则对于任意的正整数n都有Tn<m2﹣m+ ![]() 成立等价于对于任意的正整数n都有
成立等价于对于任意的正整数n都有 ![]() ≤m2﹣m+
≤m2﹣m+ ![]() 成立,
成立,
化简得:m(m﹣1)≥0,
解得:m≤或m≥1.
【解析】(1)通过在(p﹣1)Sn=p2﹣an(p>0,p≠1)中令n=1可知a1=p,令n=2可知a2=1,令n=3并结合a3= ![]() 可知p=3,进而可知数列{an}是首项为3,公比为
可知p=3,进而可知数列{an}是首项为3,公比为 ![]() 的等比数列,计算即得结论;(2)通过(1)可知bn=
的等比数列,计算即得结论;(2)通过(1)可知bn= ![]() ,裂项、并项相加可知Tn=
,裂项、并项相加可知Tn= ![]() ﹣
﹣ ![]() (
( ![]() +
+ ![]() ),利用Tn<
),利用Tn< ![]() ,问题转化为解不等式
,问题转化为解不等式 ![]() ≤m2﹣m+
≤m2﹣m+ ![]() ,计算即得结论.
,计算即得结论.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系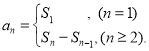 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】命题p:在△ABC中,∠C>∠B是sinC>sinB的充分必要条件;命题q:a>b是ac2>bc2的充分不必要条件( )
A.p真q假
B.p假q真
C.“p或q”为假
D.“p且q”为真
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC﹣A1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证: 
(1)直线A1E∥平面ADC1;
(2)直线EF⊥平面ADC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() 表示三条不同的直线,
表示三条不同的直线,![]() ,
,![]() ,
,![]() 表示三个不同的平面,给出下列四个命题:
表示三个不同的平面,给出下列四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,
,![]() 是
是![]() 在
在![]() 内的射影,
内的射影,![]()
![]()
![]() ,则
,则![]() ;
;
③若![]() 是平面
是平面![]() 的一条斜线,点
的一条斜线,点![]() ,
,![]() 为过点
为过点![]() 的一条动直线,则可能有
的一条动直线,则可能有![]() 且
且![]() ;
;
④若![]() ,则
,则![]() .
.
其中正确的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一三棱柱ABC﹣A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )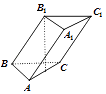
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1(﹣1,0),F2(1,0),动点M到点F2的距离是 ![]() ,线段MF1的中垂线交线段MF2于点P. (Ⅰ)当点M变化时,求动点P的轨迹G的方程;
,线段MF1的中垂线交线段MF2于点P. (Ⅰ)当点M变化时,求动点P的轨迹G的方程;
(Ⅱ)过点F2且不与x轴重合的直线L与曲线G相交于A,B两点,过点B作x轴的平行线与直线x=2相交于点C,则直线AC是否恒过定点,若是请求出该定点,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12. (Ⅰ)写出直线l的极坐标方程与曲线C的直角坐标方程;
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12. (Ⅰ)写出直线l的极坐标方程与曲线C的直角坐标方程;
(Ⅱ)已知与直线l平行的直线l'过点M(1,0),且与曲线C交于A,B两点,试求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)为奇函数,且x0是y=f(x)﹣ex的一个零点,则下列函数中,﹣x0一定是其零点的函数是( )
A.y=f(﹣x)e﹣x﹣1
B.y=f(x)ex+1
C.y=f(x)ex﹣1
D.y=f(﹣x)ex+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com