
����Ŀ������ԲC�� ![]() +
+ ![]() =1��a��b��0�������ҽ���ֱ�ΪF1��F2 �� �϶���ΪA����A��AF2��ֱ��ֱ�߽�x�Ḻ������Q�㣬��F1ǡ�����߶�QF2���е㣮
=1��a��b��0�������ҽ���ֱ�ΪF1��F2 �� �϶���ΪA����A��AF2��ֱ��ֱ�߽�x�Ḻ������Q�㣬��F1ǡ�����߶�QF2���е㣮
��1������A��Q��F2�����Բǡ����ֱ��3x��4y��7=0���У�����ԲC�ķ��̣�
��2���ڣ�1���������£�B����ԲC���㣬����R�� ![]() ��0������x��غϵ�ֱ��l����ԲC��E��F���㣬ֱ��BE��BF�ֱ�ֱ��x=
��0������x��غϵ�ֱ��l����ԲC��E��F���㣬ֱ��BE��BF�ֱ�ֱ��x= ![]() ��M��N���㣬��ֱ��MR��NR��б�ʷֱ�Ϊk1 �� k2 �� ���ʣ�k1k2�Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ���˵�����ɣ�
��M��N���㣬��ֱ��MR��NR��б�ʷֱ�Ϊk1 �� k2 �� ���ʣ�k1k2�Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������֪A��0��b����F1���߶�QF1���е㣬
��F1����c��0����F2��c��0������Q����3c��0����
�ߡ�QAF1=90�㣬
��b2=3c2��
������Rt��QAF1���ԲԲ��Ϊб�ߵ�QF1�е�F1����c��0�����뾶����2c��
��A��Q��F2������ǡ����ֱ��3x��4y��7=0���У�
��F1����c��0����ֱ�ߵľ�����ڰ뾶2c��
�� ![]() =2c��
=2c��
��ã�c=1��b2=3��a2=4��
����Բ�ı����̣� ![]()
��2��
�⣺��E��x1��y1����F��x2��y2����
ֱ��PQ�ķ���Ϊx=my+ ![]() ��������Բ����
��������Բ���� 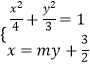 ��
��
4��4+3m2��y2+36my��21=0��
y1+y2=�� ![]() ��y1y2=��
��y1y2=�� ![]() ��
��
��B��E��M�����㹲�ߣ���֪�� ![]() =
= ![]() ����yM=
����yM= ![]() ��
��
ͬ���ɵã�yN= ![]() ��
��
��k1k2= ![]() ��
�� ![]() =
= ![]() =
= ![]() ��
��
��4��x1+2����x2+2��=��2my1+7����2my2+7��=4m2y1y2+14m��y1+y2��+49��
��k1k2=  =��
=�� ![]() ��
��
��k1k2�Ƿ�Ϊ��ֵ�� ![]()
����������1���������֪b2=3c2 �� ���ݵ㵽ֱ�ߵľ��빫ʽ���������c��ֵ�����a��b��ֵ�������Բ���̣���2����ֱ��PQ���̣�������Բ���̣�����Τ�ﶨ����ֱ�ߵ�б�ʹ�ʽ�����M��N��������꣬����б�ʹ�ʽ���k1 �� k2 �� ����Τ�ﶨ���������k1k2 ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC�У�B����1��0����C��1��0������|AB|+|AC|=4��
������A�Ĺ켣M�ķ��̣�
����PΪ�켣M�϶��㣬��PBC������Բ���ΪS1 �� ���Բ���ΪS2 �� ��P��M���˶�ʱ���� ![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����fn��x��=a1x+a2x2+a3x3+��+anxn �� ��fn����1��=����1��nn��n��N* �� �躯��g��n��=  ����bn=g��2n+4����n��N* �� ������{bn}��ǰn��n��2�����Sn���� ��
����bn=g��2n+4����n��N* �� ������{bn}��ǰn��n��2�����Sn���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ߵĶ���������ԭ�㣬����F��y���������ϣ�����F��ֱ�߽���������A��B���㣬�߶�AB�ij���8��AB���е㵽x��ľ�����3��
��1���������ߵı����̣�
��2����ֱ��m��y���ϵĽؾ�Ϊ6�����������߽���P��Q���㣬����QF���ӳ��������ߵ����ڵ�R����ֱ��PRǡ������������ʱ����ֱ��m�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ABC���������㶼������ΪO���뾶Ϊ3�������ϣ�������O��ABC�ĸ�Ϊ2����D���߶�BC���е㣬����D����O�Ľ��棬����������СֵΪ�� ��
A.![]()
B.4��
C.![]()
D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����a��b��a��c����ABC�����Բ�뾶Ϊ1�� ![]() ������BC��һ��D����BD=2DC���ҡ�BAD=90�㣬���ABC�����Ϊ ��
������BC��һ��D����BD=2DC���ҡ�BAD=90�㣬���ABC�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x+2|��|x��2|+m��m��R����
������m=1����ʽf��x����0�Ľ⼯��
����������f��x��=x������ʵ������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ζ�ȫ��50��ѧ����ѧϰ�����ԺͶԴ��༶������̬�Ƚ����˵��飬ͳ�����������ʾ��
�����μӰ༶���� | ��̫�����μӰ༶���� | �ϼ� | |
ѧϰ�����Ը� | 18 | 7 | 25 |
ѧϰ������һ�� | 6 | 19 | 25 |
�ϼ� | 24 | 26 | 50 |
�������������������һ��ѧ������ô�鵽�����μӰ༶������ѧ���ĸ����Ƕ��٣��鵽��̫�����μӰ༶������ѧϰ������һ���ѧ���ĸ����Ƕ��٣�
���������ö����Լ����˼�뷽��������ѧ����ѧϰ��������Դ��༶������̬���Ƿ��йأ���˵�����ɣ�
�ο���ʽ���ٽ�ֵ����K2= ![]() ��
��
p��K2��k0�� | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��f��x��=sin��2x�� ![]() ����cos2x��
����cos2x��
��������f��x������С�����ڡ����ֵ��ȡ�����ֵʱx�ļ��ϣ�
�������ABC�ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c���� ![]() ��b=1��
��b=1�� ![]() ����a��b�����B�ͽ�C��
����a��b�����B�ͽ�C��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com