
【题目】改革开放40年来,我国城市基础设施发生了巨大的变化,各种交通工具大大方便了人们的出行需求.某城市的A先生实行的是早九晚五的工作时间,上班通常乘坐公交或地铁加步行.已知从家到最近的公交站或地铁站都需步行5分钟,乘坐公交到离单位最近的公交站所需时间Z1(单位:分钟)服从正态分布N(33,42),下车后步行再到单位需要12分钟;乘坐地铁到离单位最近的地铁站所需时间Z2(单位:分钟)服从正态分布N(44,22),从地铁站步行到单位需要5分钟.现有下列说法:①若8:00出门,则乘坐公交一定不会迟到;②若8:02出门,则乘坐公交和地铁上班迟到的可能性相同;③若8:06出门,则乘坐公交比地铁上班迟到的可能性大;④若8:12出门,则乘坐地铁比公交上班迟到的可能性大.则以上说法中正确的序号是_____.
参考数据:若Z~N(μ,σ2),则P(μ﹣σ<Z≤μ+σ)=0.6826,P(μ﹣2σ<Z≤μ+2σ)=0.9544,P(μ﹣3σ<Z≤μ+3σ)=0.9974
【答案】②④
【解析】
利用正态分布对每一个说法求解其概率,逐项分析,即可选出正确答案.
解:①若8:00出门,江先生乘坐公交,从家到车站需要5分钟,下车后步行再到单位需要12分钟,
乘坐公交到离单位最近的公交站所需时间![]() 服从正态分布
服从正态分布![]() ,
,
故![]()
![]() ,
,
∴江先生仍有可能迟到,只不过概率较小,故①错误;
②若8:02出门,江先生乘坐公交,
∵从家到车站需要5分钟,下车后步行再到单位需要12分钟,
乘坐公交到离单位最近的公交站所需时间![]() 服从正态分布
服从正态分布![]() ,
,
故当满足P(Z≤41)![]() 时,江先生乘坐公交不会迟到;
时,江先生乘坐公交不会迟到;
若8:02出门,江先生乘坐地铁,
∵从家到车站需要5分钟,下地铁后步行再到单位需要5分钟,
乘坐地铁到离单位最近的地铁站所需时间![]() 服从正态分布
服从正态分布![]() ,
,
故当满足P(Z≤48)![]() 时,江先生乘坐地铁不会迟到,
时,江先生乘坐地铁不会迟到,
此时两种上班方式江先生不迟到的概率相当,故②正确;
③若8:06出门,江先生乘坐公交,
∵从家到车站需要5分钟,下车后步行再到单位需要12分钟,
乘坐公交到离单位最近的公交站所需时间![]() 服从正态分布
服从正态分布![]() ,
,
故当满足![]() 时,江先生乘坐公交不会迟到;
时,江先生乘坐公交不会迟到;
若8:06出门,江先生乘坐地铁,
∵从家到车站需要5分钟,下地铁后步行再到单位需要5分钟,
乘坐地铁到离单位最近的地铁站所需时间![]() 服从正态分布
服从正态分布![]() ,
,
故当满足![]() 时,江先生乘坐地铁不会迟到,
时,江先生乘坐地铁不会迟到,
此时两种上班方式,乘坐公交比地铁上班迟到的可能性小,故③错误;
④若8:12出门,江先生乘坐公交,
∵从家到车站需要5分钟,下车后步行再到单位需要12分钟,
乘坐公交到离单位最近的公交站所需时间![]() 服从正态分布
服从正态分布![]() ,
,
故当满足![]() 时,江先生乘坐公交不会迟到,
时,江先生乘坐公交不会迟到,
而![]() ;
;
若8:12出门,江先生乘坐地铁,
∵从家到车站需要5分钟,下地铁后步行再到单位需要5分钟,
乘坐地铁到离单位最近的地铁站所需时间![]() 服从正态分布
服从正态分布![]() ,
,
故当满足![]() 时,江先生乘坐地铁不会迟到,
时,江先生乘坐地铁不会迟到,
由![]() ,
,
∴若8:12出门,则乘坐地铁比公交上班迟到的可能性大,故④正确;
故答案为:②④.


科目:高中数学 来源: 题型:
【题目】已知两动圆![]() 和
和![]() (
(![]() ),把它们的公共点的轨迹记为曲线
),把它们的公共点的轨迹记为曲线![]() ,若曲线
,若曲线![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,且曲线
,且曲线![]() 上的相异两点
上的相异两点![]() 满足:
满足:![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)证明直线![]() 恒经过一定点,并求此定点的坐标;
恒经过一定点,并求此定点的坐标;
(3)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为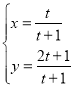 (t为参数),曲线C2的参数方程为
(t为参数),曲线C2的参数方程为![]() (α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;
(Ⅱ)射线![]() 与曲线C2交于O,P两点,射线
与曲线C2交于O,P两点,射线![]() 与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌赛马是《史记》中记载的一个故事,说的是齐国大将军田忌经常与齐国众公子赛马,孙膑发现田忌的马和其他人的马相差并不远,都分为上、中、下三等.于是孙膑给田忌将军献策:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得了许多赌注.假设田忌的各等级马与某公子的各等级马进行一场比赛,田忌获胜的概率如下表所示:
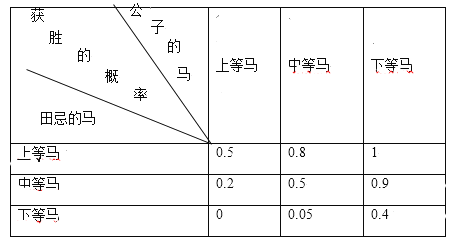
比赛规则规定:一次比赛由三场赛马组成,每场由公子和田忌各出一匹马参赛,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
(1)如果按孙膑的策略比赛一次,求田忌获胜的概率;
(2)如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com