
| A�� | $\frac{1}{2}$��$\frac{11}{32}$ | B�� | $\frac{1}{2}$��$\frac{31}{32}$ | C�� | $\frac{11}{32}$��$\frac{31}{32}$ | D�� | $\frac{11}{32}$��$\frac{5}{2}$ |
���� �ɵȱ�����ǰn���ʽ��q4+q2-20=0���Ӷ�q=��2���ɴ����������{$\frac{1}{{a}_{n}}$}��ǰ5��ͣ�
��� �⣺�ߵȱ�����{an}��ǰn��ΪSn��a1=2��$\frac{{S}_{6}}{{S}_{2}}$=21��
��$\frac{{S}_{6}}{{S}_{2}}$=$\frac{{a}_{1}��1-{q}^{6}��}{{a}_{1}��1-{q}^{2}��}$=$\frac{1-{q}^{6}}{1-{q}^{2}}$=21��
��$\frac{��1-{q}^{3}����1+{q}^{3}��}{��1-q����1+q��}$=��1+q+q2����1-q+q2��=��1+q2��2-q2=21��
��������q4+q2-20=0��
���q=��2��
��q=2ʱ��${a}_{n}=2��{2}^{n-1}={2}^{n}$������{$\frac{1}{{a}_{n}}$}��ǰ5���Ϊ${S}_{5}=\frac{\frac{1}{2}��1-\frac{1}{{2}^{5}}��}{1-\frac{1}{2}}=\frac{31}{32}$
��q=-2ʱ��an=2����-2��n-1������{$\frac{1}{{a}_{n}}$}��ǰ5���Ϊ${S}_{5}=\frac{\frac{1}{2}[1-��-\frac{1}{2}��^{5}]}{1-��-\frac{1}{2}��}$=$\frac{11}{32}$��
������{$\frac{1}{{a}_{n}}$}��ǰ5���Ϊ$\frac{11}{32}$��$\frac{31}{32}$��
��ѡ��C��
���� ���⿼��ȱ����е�ǰ5��͵������е��⣬����ʱ�������⣬ע��ȱ����е����ʵĺ������ã�


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{1}{2}$] | B�� | [2��+�ޣ� | C�� | ��0��2] | D�� | ��-�ޣ�2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
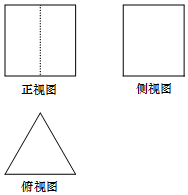 ij�����������ͼ��ͼ��ʾ����������ͼ�DZ߳�Ϊ2�������Σ�����ͼ���������Σ�����������������ǣ�������
ij�����������ͼ��ͼ��ʾ����������ͼ�DZ߳�Ϊ2�������Σ�����ͼ���������Σ�����������������ǣ�������| A�� | $2\sqrt{3}$ | B�� | $4\sqrt{3}$ | C�� | $\frac{2}{3}\sqrt{3}$ | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
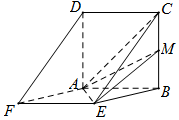 ��֪�߳�Ϊ2��������ABCD������ABEF����ƽ�滥�ഹֱ��MΪBC�е㣮
��֪�߳�Ϊ2��������ABCD������ABEF����ƽ�滥�ഹֱ��MΪBC�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
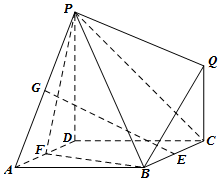 ��ͼ��ʾ�Ķ������У���ABCD�DZ߳�Ϊ2�������Σ�ƽ��PDCQ��ƽ��ABCD��PD��DC��E��F��G�ֱ�Ϊ��BC��AD��PA���е㣮
��ͼ��ʾ�Ķ������У���ABCD�DZ߳�Ϊ2�������Σ�ƽ��PDCQ��ƽ��ABCD��PD��DC��E��F��G�ֱ�Ϊ��BC��AD��PA���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
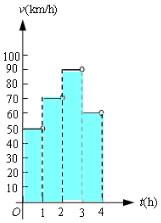 һ��������ij��·���е���ʻ������ʱ��Ĺ�ϵ��ͼ��ʾ��
һ��������ij��·���е���ʻ������ʱ��Ĺ�ϵ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | $\frac{5}{2}$ | C�� | 2 | D�� | 7 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com