
【题目】已知函数![]() ,
,![]()
(1)当![]() 时,求
时,求![]() 的单调增区间.
的单调增区间.
(2)若对任意的实数![]() 及任意的
及任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)将![]() 时,可得f(x)解析式,根据二次函数图象特征可得f(x)的单调增区间;
时,可得f(x)解析式,根据二次函数图象特征可得f(x)的单调增区间;
(2)结合绝对值不等式的性质,利用构造函数法进行求解即可.
(1)当![]() 时,f(x)=
时,f(x)=![]() x2+|x
x2+|x![]() |+b=
|+b=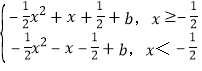 ,
,
当![]() 时,对称轴x=1,开口向下;f(x)的单调增区间为
时,对称轴x=1,开口向下;f(x)的单调增区间为![]() ;
;
当x![]() 时,对称轴x=﹣1,开口向下;f(x)的单调增区间为
时,对称轴x=﹣1,开口向下;f(x)的单调增区间为![]() ;
;
综上可得f(x)的单调增区间为![]() .
.
(2)因为|f(x)|≤2,所以﹣2≤ax2+|x﹣a|+b≤2,
又因为对任意的实数b∈[0,1]及任意的x∈[﹣3,3],上式恒成立,
所以﹣2≤ax2+|x﹣a|≤1,(*),
记g(x)=ax2+|x﹣a|,
所以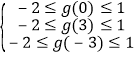 ,可得﹣
,可得﹣![]() ≤a≤﹣
≤a≤﹣![]() ,
,
又(*)式可化为﹣ax2﹣2≤|x﹣a|≤﹣ax2+1,
记h1(x)=﹣ax2+1,h2(x)=﹣ax2﹣2,k(x)=|x﹣a|,
由﹣![]() ≤a≤﹣
≤a≤﹣![]() ,可知,h2(x)<0,
,可知,h2(x)<0,
所以命题转化为:只需满足以下条件
①﹣ax2﹣2=﹣x+a的较小根小于或等于﹣3,
②﹣ax2+1=x﹣a的较小根大于或等于3(或是无实根),
由①得![]() ≤﹣3,解得﹣
≤﹣3,解得﹣![]() ≤a≤0;
≤a≤0;
由②得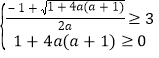 或1+4a(a+1)≤0,解得a=﹣
或1+4a(a+1)≤0,解得a=﹣![]() ,
,
综上可知a的取值范围是a=﹣![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上减函数;
为R上减函数;
(2) 若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() (-2)=0,则
(-2)=0,则![]() >0解集为(-2,2);
>0解集为(-2,2);
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)若一个函数定义域![]() 且
且![]() 的奇函数,当
的奇函数,当![]() 时,
时,![]() ,则当x<0时
,则当x<0时![]() ,其中正确的是____________________
,其中正确的是____________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工厂需要围建一个面积为512![]() 的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度
的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度![]() (单位:
(单位: ![]() )是利用原有墙壁长度
)是利用原有墙壁长度![]() (单位:
(单位: ![]() )的函数.
)的函数.
(1)写出![]() 关于
关于![]() 的函数解析式,确定
的函数解析式,确定![]() 的取值范围.
的取值范围.
(2)堆料场的长、宽之比为多少时,需要砌起的新墙用的材料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
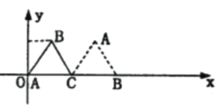
【题目】如图放置的边长为2的正三角形![]() 沿
沿![]() 轴滚动, 设顶点
轴滚动, 设顶点![]() 的纵坐标与横坐标的函数关系式是
的纵坐标与横坐标的函数关系式是![]() , 有下列结论:
, 有下列结论:
①函数![]() 的值域是
的值域是![]() ;②对任意的
;②对任意的![]() ,都有
,都有![]() ;
;
③函数![]() 是偶函数;④函数
是偶函数;④函数![]() 单调递增区间为
单调递增区间为![]() .
.
其中正确结论的序号是________. (写出所有正确结论的序号)
说明:
“正三角形![]() 沿
沿![]() 轴滚动”包括沿
轴滚动”包括沿![]() 轴正方向和沿
轴正方向和沿![]() 轴负方向滚动. 沿
轴负方向滚动. 沿![]() 轴正方向滚动指的是先以顶点
轴正方向滚动指的是先以顶点![]() 为中心顺时针旋转, 当顶点
为中心顺时针旋转, 当顶点![]() 落在
落在![]() 轴上时, 再以顶点
轴上时, 再以顶点![]() 为中心顺时针旋转, 如此继续. 类似地, 正三角形
为中心顺时针旋转, 如此继续. 类似地, 正三角形![]() 可以沿
可以沿![]() 轴负方向滚动.
轴负方向滚动.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣4|,g(x)=|2x+1|.
(1)解不等式f(x)<g(x);
(2)若2f(x)+g(x)>ax对任意的实数x恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com