
分析 (1)由条件利用正弦函数的定义域和值域求得函数f(x)的值域.
(2)令$f(x)=2sin(2x-\frac{π}{3})=1$,求得x的值,可得结论.
解答 解:(1)f(x)=$2sinxcosx-2\sqrt{3}{cos^2}x+\sqrt{3}$=$sin2x-\sqrt{3}cos2x=2sin(2x-\frac{π}{3})$,
当$x∈[0,\frac{π}{2}]$时,$2x-\frac{π}{3}∈[-\frac{π}{3},\frac{2π}{3}]$,所以f(x)的值域为$[-\sqrt{3},2]$.
(2)令$f(x)=2sin(2x-\frac{π}{3})=1$,∴$sin(2x-\frac{π}{3})=\frac{1}{2}$,故 $2x-\frac{π}{3}=2kπ+\frac{π}{6}$或$2x-\frac{π}{3}=2kπ+\frac{5π}{6}$,k∈Z,
∴当函数y=f(x)的图象和直线 y=1时的两交点的最短距离为$\frac{π}{3}$.
点评 本题主要考查正弦函数的定义域和值域,函数的零点与方程的根的关系,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
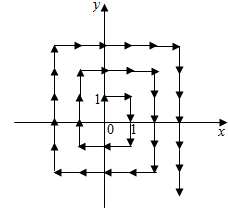 如图,将自然数按如下规则“放置”在平面直角坐标系中,使其满足条件:①每个自然数“放置”在一个“整点”(横纵坐标均为整数的点)上;②0在原点,1在(0,1)点,2在(1,1)点,3在(1,0)点,4在(1,-1)点,5在(0,-1)点,…,即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上,则放置数字(2n+1)2,n∈N*的整点坐标是(-n,n+1).
如图,将自然数按如下规则“放置”在平面直角坐标系中,使其满足条件:①每个自然数“放置”在一个“整点”(横纵坐标均为整数的点)上;②0在原点,1在(0,1)点,2在(1,1)点,3在(1,0)点,4在(1,-1)点,5在(0,-1)点,…,即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上,则放置数字(2n+1)2,n∈N*的整点坐标是(-n,n+1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com