
 :
: 是奇函数,因为f(x)的定义域为R,
是奇函数,因为f(x)的定义域为R,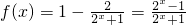 ,则
,则 ,
,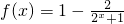 ,因为2x+1在R上递增,所以
,因为2x+1在R上递增,所以 在R上递减,所以
在R上递减,所以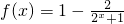 在R上递增.
在R上递增. ,
, ,
,

科目:高中数学 来源:北京五中2007-2008学年度第一学期期中考试试卷高三数学(理科) 题型:013
对于函数 ,下列结论正确的是
,下列结论正确的是
A.函数f(x)的值域是[-1,1]
B.当且仅当![]() 时,f(x)取最大值1
时,f(x)取最大值1
C.函数f(x)是以2π为最小正周期的周期函数
D.当且仅当![]() (k∈Z)时,f(x)<0
(k∈Z)时,f(x)<0
查看答案和解析>>
科目:高中数学 来源:2006学年浙江省余杭中学一摸备考(四)(理科数学) 题型:013
对于函数![]() ,下列叙述正确的是
,下列叙述正确的是
A.既有极大值又有最大值
B.有极大值但没有最大值
C.没有极大值但有最大值
D.既无极大值又无最大值
查看答案和解析>>
科目:高中数学 来源:2008年高考预测卷理科数学(广东卷)全国通用 题型:013
设a>0,对于函数![]() ,下列结论正确的是
,下列结论正确的是
A.有最大值而无最小值
B.有最小值而无最大值
C.有最大值且有最小值
D.既无最大值又无最小值
查看答案和解析>>
科目:高中数学 来源:2007-2008学年度北京市第五中学第一学期高三数学期中考试试卷(理) 题型:013
对于函数 ,下列结论正确的是
,下列结论正确的是
A.函数f(x)的值域是[-1,1]
B.当且仅当![]() 时,f(x
时,f(x![]() 取最大值1
取最大值1
C.函数f(x)是以2π为最小正周期的周期函数
D.当且仅当![]() (k∈Z)时,f(x)<0
(k∈Z)时,f(x)<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com