
【题目】已知某款冰淇淋的包装盒为圆台,盒盖为直径为![]() 的圆形纸片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一个,假定每个冰淇淋球都是半径为
的圆形纸片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一个,假定每个冰淇淋球都是半径为![]() 的球体,三个冰淇淋球两两相切,且都与冰淇淋盒盖、盒底和盒子侧面的曲面相切,则冰淇淋盒的体积为______.
的球体,三个冰淇淋球两两相切,且都与冰淇淋盒盖、盒底和盒子侧面的曲面相切,则冰淇淋盒的体积为______.
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,过
,过![]() 点作
点作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() ,交
,交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
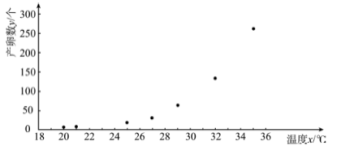
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款,法国8款,荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国.A地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区有6家婴幼儿用品商店在售这几种品牌的奶粉,甲、乙、丙3名检测员分别负责进行检测,每人至少抽检1家商店,且检测过的商店不重复检测,则甲检测员检测2家商店的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国数学家布丰提出一种计算圆周率![]() 的方法——随机投针法,受其启发,我们设计如下实验来估计
的方法——随机投针法,受其启发,我们设计如下实验来估计![]() 的值:先请200名同学每人随机写下一个横、纵坐标都小于1的正实数对
的值:先请200名同学每人随机写下一个横、纵坐标都小于1的正实数对![]() ;再统计两数的平方和小于1的数对
;再统计两数的平方和小于1的数对![]() 的个数
的个数![]() ;最后再根据统计数
;最后再根据统计数![]() 来估计
来估计![]() 的值.已知某同学一次试验统计出
的值.已知某同学一次试验统计出![]() ,则其试验估计
,则其试验估计![]() 为______.
为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 的离心率是
的离心率是![]() ,左右焦点分别为
,左右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过
过![]() 时,
时,![]() 的周长为
的周长为![]() .
.
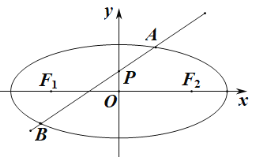
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 时,求直线
时,求直线![]() 方程;
方程;
(3)已知点![]() ,直线
,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .问是否存在实数
.问是否存在实数![]() ,使得
,使得![]() 恒成立?
恒成立?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,过
,过![]() (M不过椭圆的顶点和中心)且斜率为k直线l交椭圆于
(M不过椭圆的顶点和中心)且斜率为k直线l交椭圆于![]() 两点,与y轴交于点N,且
两点,与y轴交于点N,且![]() .
.
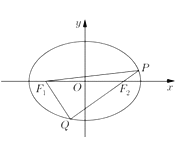
(1)若直线l过点![]() ,求
,求![]() 的周长;
的周长;
(2)若直线l过点![]() ,求线段
,求线段![]() 的中点R的轨迹方程;
的中点R的轨迹方程;
(3)求证:![]() 为定值,并求出此定值.
为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:ax+![]() y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D,给出下面三个结论:①a≥1,S△AOB=
y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D,给出下面三个结论:①a≥1,S△AOB=![]() ;②a≥1,|AB|<|CD|;③a≥1,S△COD<
;②a≥1,|AB|<|CD|;③a≥1,S△COD<![]() .其中,所有正确结论的序号是( )
.其中,所有正确结论的序号是( )
A.①②B.②③C.①③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,记集合
,记集合![]() .
.
(1)对于数列![]() ,写出集合
,写出集合![]() ;
;
(2)若![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?若存在,求出一组符合条件的
?若存在,求出一组符合条件的![]() ;若不存在,说明理由.
;若不存在,说明理由.
(3)若![]() ,把集合
,把集合![]() 中的元素从小到大排列,得到的新数列为
中的元素从小到大排列,得到的新数列为![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com