
【题目】如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,角∠AOB= ![]() ,若点A的坐标为(
,若点A的坐标为( ![]() ,
, ![]() ),记∠COA=α.
),记∠COA=α. 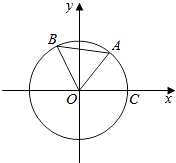
(1)求 ![]() 的值;
的值;
(2)求点B的坐标.
【答案】
(1)解:∵A的坐标为( ![]() ,
, ![]() ),根据三角函数的定义可知:sinα=
),根据三角函数的定义可知:sinα= ![]() ,cosα=
,cosα= ![]() ,
,
∴ ![]() =
= ![]() =32
=32
(2)解:∵角∠AOB= ![]() ,
,
∴cos∠COB=cos(α+ ![]() )=cosαcos
)=cosαcos ![]() ﹣sinαsin
﹣sinαsin ![]() =﹣
=﹣ ![]() ,
,
∴sin∠COB=sin(α+ ![]() )=sinαcos
)=sinαcos ![]() +cosαsin
+cosαsin ![]() =
= ![]() ,
,
∴点B(﹣ ![]() ,
, ![]() )
)
【解析】(1)由已知,根据三角函数的定义可求sinα,cosα的值,利用二倍角公式即可计算得解.(2)利用特殊角的三角函数值,两角和的正弦函数余弦函数公式分别求出cos∠COB,sin∠COB的值即可得解.
【考点精析】认真审题,首先需要了解同角三角函数基本关系的运用(同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C=![]() ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值,并指出极大值还是极小值;
的极值,并指出极大值还是极小值;
(2)若![]() ,求函数
,求函数![]() 在
在![]() 上的最值;
上的最值;
(3)若![]() ,求证:在区间
,求证:在区间![]() 上,函数
上,函数![]() 的图象在
的图象在![]() 的图象下方.
的图象下方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客运公司用A,B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次.A,B两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1600元/辆和2400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A型车7辆.若每天要以不少于900人运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某类体育节目的收视情况,随机抽取了100名观众进行调查,如图是根据调查结果绘制的观众日均收看该类体育节目时间的频率分布直方图,其中收看时间分组区间是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].将日均收看该类体育节目时间不低于40分钟的观众称为“体育迷”.则抽取的100名观众中“体育迷”有名. 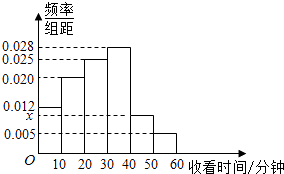
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题. 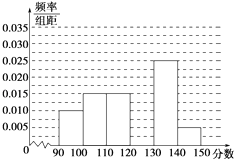
(1)从该校高三模拟考试的成绩中随机抽取一份,利用随机事件频率估计概率,求数学分数恰在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2﹣a≥0,命题q:x0∈R,使得x02+(a﹣1)x0﹣1<0,若p∨q为真,p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数y=sin4θ﹣cos4θ的最小正周期是π;
②终边在y轴上的角的集合是 ![]() ;
;
③把 ![]() 的图象向右平移
的图象向右平移 ![]() 得到y=3sin2x的图象;
得到y=3sin2x的图象;
④函数 ![]() 在[0,π]是减函数;
在[0,π]是减函数;
其中真命题的序号是(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设对于任意实数x,不等式|x+7|+|x﹣1|≥m恒成立.
(1)求m的取值范围;
(2)当m取最大值时,解关于x的不等式:|x﹣3|﹣2x≤2m﹣12.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com