
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
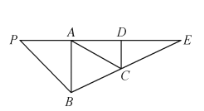
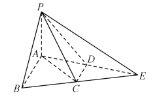
【题目】如图,在![]() 中,
中,![]() ,D是AE的中点,C是线段BE上的一点,且
,D是AE的中点,C是线段BE上的一点,且![]() ,
,![]() ,将
,将![]() 沿AB折起使得二面角
沿AB折起使得二面角![]() 是直二面角.
是直二面角.
(l)求证:CD平面PAB;
(2)求直线PE与平面PCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A. 在数列|![]() 中,
中,![]() 由此归纳出
由此归纳出![]() 的通项公式
的通项公式
B. 由平面三角形的性质,推测空间四面体性质
C. 某校高二共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人
D. 两条直线平行,同旁内角互补,如果![]() 和
和![]() 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)在R上是单调递减的一次函数,且f(f(x))=4x-1.
(1)求f(x);
(2)求函数y=f(x)+x2-x在x∈[-1,2]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 的线性回归直线方程为
的线性回归直线方程为![]() ,且
,且![]() ,
,![]() 之间的一组相关数据如下表所示,则下列说法错误的为
之间的一组相关数据如下表所示,则下列说法错误的为

A.变量![]() ,
,![]() 之间呈现正相关关系B.可以预测,当
之间呈现正相关关系B.可以预测,当![]() 时,
时,![]()
C.![]() D.由表格数据可知,该回归直线必过点
D.由表格数据可知,该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,动点M到两定点A(﹣1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C. 
(1)求轨迹C的方程;
(2)设直线y=﹣2x+m与y轴交于点P,与轨迹C相交于点Q、R,且|PQ|<|PR|,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,其中
,其中![]() .
.
(1)写出集合![]() 中的所有元素;
中的所有元素;
(2)设![]() ,证明“
,证明“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
(3)设集合![]() ,设
,设![]() ,使得
,使得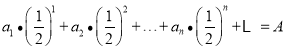 ,且
,且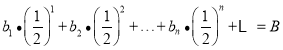 ,试判断“
,试判断“![]() ”是“
”是“![]() ”的什么条件并说明理由.
”的什么条件并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时, ![]() 的坐标为 .
的坐标为 . 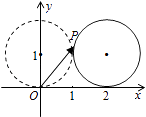
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com